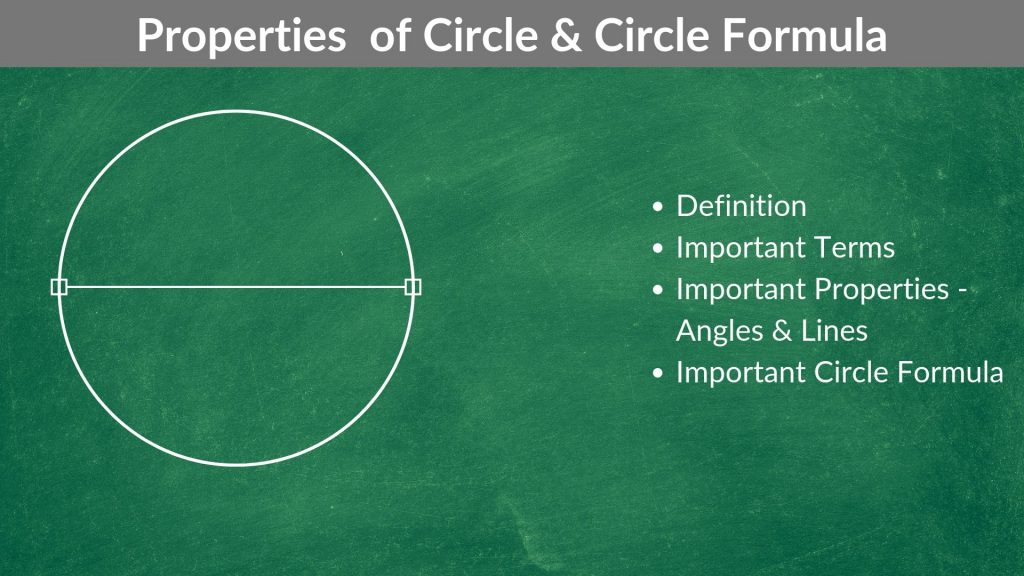
A circle is a closed shape formed by tracing a point that moves in a plane such that its distance from a given point is constant. The word circle is derived from the Greek word kirkos, meaning hoop or ring. In this article, we cover the various circle formulas, properties of a circle & important terms related to circles.
Geometry is an essential topic to ace if you plan to score 700+ on the GMAT. Let us help you achieve mastery in GMAT Geometry. Start by signing up for a free trial, get access to 400+ practice questions, and learn from the best in the industry. After all, we are the most reviewed company on GMATClub.
Richa, Guillermo, Sireesh, and Raghav are just a few of the students that have achieved a Q50+ score in the GMAT Quant section using e-GMAT. If you too wish to score Q50+ on the GMAT, here’s how we can help!
Definition of a Circle
When a set of all points that are at a fixed distance from a fixed point are joined then the geometrical figure obtained is called circle.
Let us now learn a bit about the terminology used in circles.
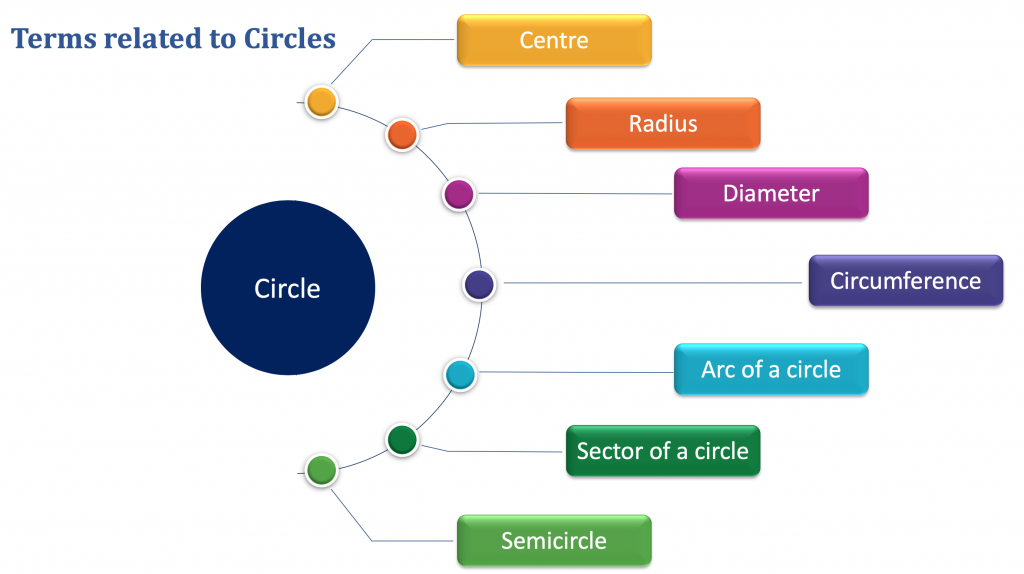
Terms related to Circles & Circle formulas
Take a free GMAT mock to understand your baseline score and start your GMAT prep with our free trial. We are the most reviewed online GMAT Prep company with 2500+ reviews on GMATClub.
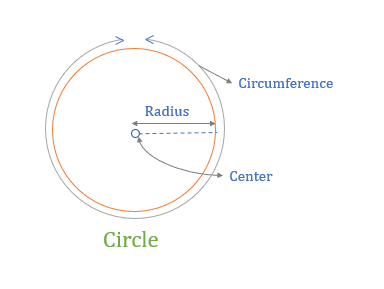
Center
The fixed point in the circle is called the center.
- So, the set of points are at a fixed distance from the center of the circle.
Radius
Radius is the fixed distance between the center and the set of points. It is denoted by “R”.
Diameter
The diameter is a line segment, having boundary points of circles as the endpoints and passing through the center.
- So, logically a diameter can be broken into two parts:
- One part from one boundary point of the circle to the center
- And, the other part from the center to another boundary point.
- Hence, Diameter = Twice the length of the radius or “D = 2R”
Circumference
It is the measure of the outside boundary of the circle.
So, the length of the circle or the perimeter of the circle is called Circumference.
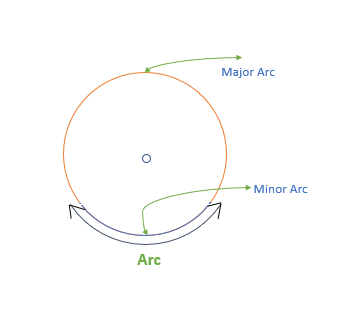
Arc of a circle
The arc of a circle is a portion of the circumference.
From any two points that lie on the boundary of the circle, two arcs can be created: A Minor and a Major Arc.
- Minor arc: The shorter arc created by two points.
- Major Arc: The longer arc created by two points.
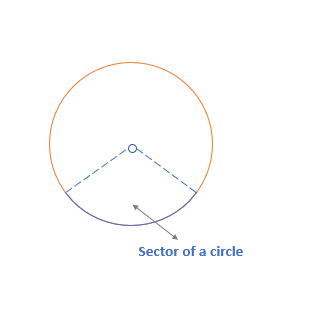
Sector of a circle:
A Sector is formed by joining the endpoints of an arc with the center.
- On joining the endpoints with the center, two sectors will be obtained: Minor and Major.
- By default, we only consider the Minor sector unless it is mentioned otherwise.
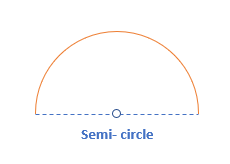
Semi-circle
A semi-circle is half part of the circle or,
- A semi-circle is obtained when a circle is divided into two equal parts.
Now that we know all the terminologies related to the circles, let us learn about the properties of a circle.
Geometry is an essential topic to ace if you plan to score 700+ on the GMAT. Let us help you achieve mastery in GMAT Geometry. Start by signing up for a free trial and learn from the best in the industry. After all, we are the most reviewed company on gmatclub.
Richa, Guillermo, Sireesh, and Raghav are just a few of the students that have achieved a Q50+ score in the GMAT Quant section using e-GMAT. Get started with our free trial today if you too wish to score Q50+ on the GMAT!
Important Properties of Circles – Related to Lines
Properties related to Lines in a Circle | Properties of circle
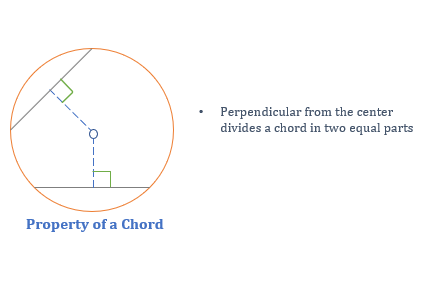
Chord
A chord is a line segment whose endpoints lie on the boundary of the circle.

Properties of Chord
- Perpendicular dropped from the center divides a chord into two equal parts.
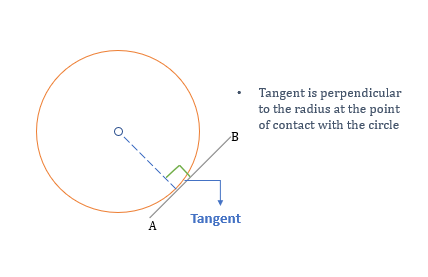
Tangent
Tangent is a line that touches the circle at any point.
Properties of Tangent
- Radius is always perpendicular to the tangent at the point where it touches the circle.
Important Properties of Circles – Related to Angles
Did you know a GMAT score of 730+ yields an incremental $500K in ROI? Start your GMAT Preparation by Signing up for our FREE Trial and get access to FREE online GMAT preparation resources. We are the most reviewed GMAT preparation company on GMATClub with more than 2500 reviews.
Properties related to Angles in a circle | Properties of Circle
Inscribed Angle
An inscribed angle is the angle formed between two chords when they meet on the boundary of the circle.

Properties of Inscribed Angles
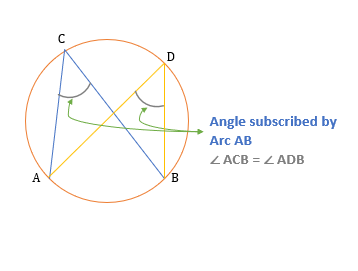
1. Angles formed by the same arc on the circumference of the circle is always equal.
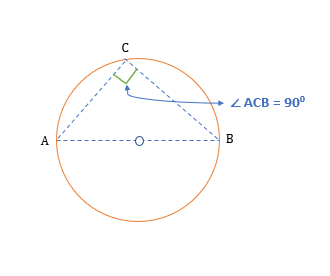
2. The angle in a semi-circle is always 90°.Central Angle
A central angle is the angle formed when two-line segments meet such that one of the endpoints of both the line segment is at the center and another is at the boundary of the circle.
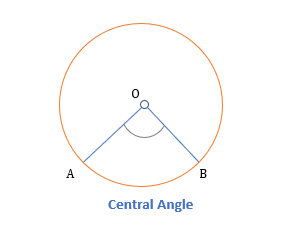
Property of Central Angles
- An angle formed by an arc at the center is twice the inscribed angle formed by the same arc.

Important Circle Formulas: Area and Perimeter
The following are some mathematical formulae that will help you calculate the area and perimeter/circumference of a circle.
Perimeter:
- Perimeter or the Circumference of the circle = 2 × π × R.
- Length of an Arc = (Central angle made by the arc/360°) × 2 × π × R.
Area:
- Area of the circle = π × R²
- Area of the sector =(Central angle made by the sector/360°) × π × R².
Summary of all the Properties of a Circle
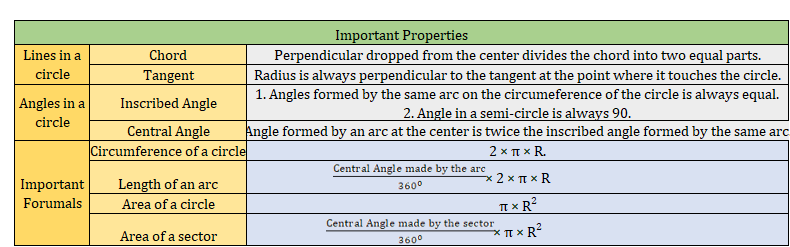
Here is a summarized list of all the properties we have learned in the article up to this point.
| Property | Element | Description |
| Lines in a circle | Chord | Perpendicular dropped from the center divides the chord into two equal parts. |
| Tangent | The radius is always perpendicular to the tangent at the point where it touches the circle. | |
| Angles in a circle | Inscribed Angle | 1. Angles formed by the same arc on the circumference of the circle is always equal. 2. The angle in a semi-circle is always 90. |
| Central Angle | The angle formed by an arc at the center is twice the inscribed angle formed by the same arc. | |
| Important Formulae | Circumference of a circle | 2 × π × R. |
| Length of an arc | (Central angle made by the arc/360°) × 2 × π × R | |
| Area of a circle | π × R² | |
| Area of a sector | (Central angle made by the arc/360°) × π × R² |
Begin your GMAT preparation with the only prep company that has delivered more 700+ scores than any other GMAT club partner. Achieve GMAT 740+ with our AI driven tools that you personilzed feedback at every step of your GMAT journey. Take our free trial today!
Application of the circle properties & circle formulas in the questions
Question 1
The lengths of two sides in a right-angle triangle other than hypotenuse are 6 cm and 8 cm. If this right-angle triangle is inscribed in a circle, then what is the area of the circle?
- 5 π
- 10 π
- 15 π
- 20 π
- 25 π
Solution
Step 1: Given
- The lengths of two sides other than hypotenuse of a right triangle are 6 cm and 8 cm.
- This triangle is inscribed in a circle.
Step 2: To find
- Area of the circle.
Step 3: Approach and Working out
Let us draw the diagrammatic representation.
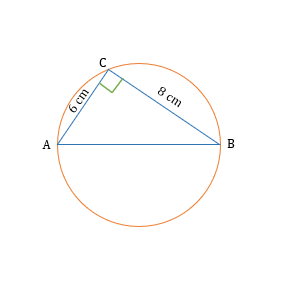
By applying the property that the angle in a semi-circle is 90º, we can say that AB is the diameter of the circle.
- And, once we find the length of the diameter, we can find the radius, and then we can find the area of the circle as well.
Applying Pythagoras theorem in △ ABC,
- AB² = AC² + BC²
- AB² = 6² + 8² = 36 +64 = 100
- AB = 10 cm
Since AB is the diameter, AB = 2R = 10
- Hence, R = 5 cm.
Area of the circle = π × R²= π × 5² = 25 π.
Hence, the correct answer is option E.
Question 2
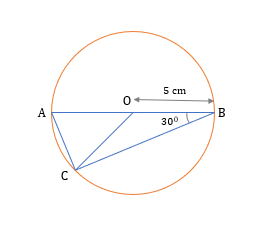
In the diagram given above, O is the center of the circle. If OB = 5 cm and ∠ABC = 300 then what the length of the arc AC?
- 5π/6
- 5π/3
- 5π/2
- 5π
- 10π
Solution
Step 1: Given
- OB = 5 cm
- ∠ABC = 30°
Step 2: To find
- Length of the arc
Step 3: Approach and Working out
- Length of the arc = (Central angle made by the arc/360°) × 2 × π × R.
To find the length of the arc, we need the value of two variable, the center angle made by the arc and the radius.
- We are already given radius as OB = 5cm
- We need to find the ∠AOC
On visualizing the diagram, the inscribed angle by the arc AC is ∠ABC, and the center angle by arc AC is ∠AOC.
- Hence, we can apply the property that the angle made at the center by an arc is twice the inscribed angle formed by the same arc.
- Thus, ∠AOC = 2 × ∠ABC = 2 × 30° = 60°
Now, we know the central angle formed by the arc as well.
- Hence, length of the arc AC =(Central angle made by the arc/360°) × 2 × π × R.
- =(60°/360°) × 2 × π × 5.
- =(1/6) × 2 × π × 5.
- =(5π/3) cm
Thus, the correct answer is option B.
For more practice questions on triangles and geometry, sign up for our free trial. We have more than 400+ practice questions and 10+ hours of AI-driven video lessons. We are the most reviewed online GMAT Prep company with 2500+ reviews on GMATClub
If you like this article here are a few more article related to geometry: