Mastering the Types of Quadrilaterals and Their Properties: A GMAT Guide

A 17 min read

Understanding quadrilateral properties is crucial for GMAT success as these concepts appear in both problem-solving and data sufficiency questions, often determining the difference between average and excellent scores.  

This comprehensive guide will build your quadrilateral knowledge from the ground up, teaching you not just what the properties are, but how they relate to each other and—most importantly—how they’re tested on the actual GMAT exam.  

Here is a video explaining the properties of quadrilaterals:

Are you struggling with GMAT quant? e-GMAT provides structured learning from foundations to help you master the skills needed for a high score. Join the world’s most successful prep company for a free trial and see the difference it can make. We are the most reviewed online GMAT Prep company with 2600+ reviews on GMATClub, as of July 2023.

Quadrilateral Fundamentals: Essential Properties of All Four-Sided Figures

What is a Quadrilateral? Definition and Basic Properties

A quadrilateral is a closed polygon with exactly four sides (edges) and four vertices (corners). The word itself gives us a clue: “quadri” means “four” and “lateral” refers to sides. If you’ve ever wondered how many sides a quadrilateral has, the answer is always four—it’s built into the name itself.

Before diving into specific types, let’s understand what properties all quadrilaterals share:

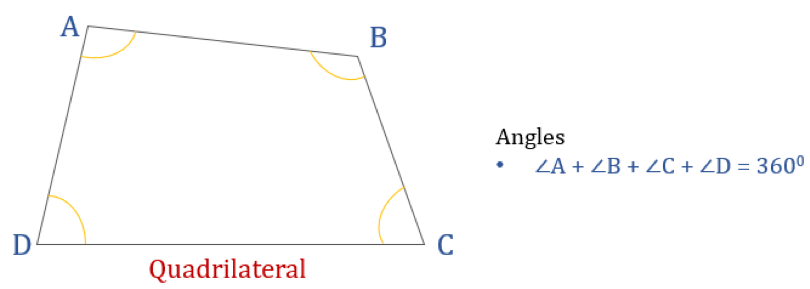
• The sum of interior angles always equals 360 degrees
• They have two diagonals connecting opposite vertices
• Any quadrilateral can be divided into two triangles by drawing either diagonal
• The sum of the exterior angles (one at each vertex) equals 360 degrees

The Angle Sum Property of Quadrilaterals

The angle sum property of quadrilaterals states that the interior angles always sum to 360 degrees. This fundamental property applies to every quadrilateral regardless of its shape or size. Understanding this property helps solve problems involving unknown angles and is often the first step in approaching many GMAT geometry questions.

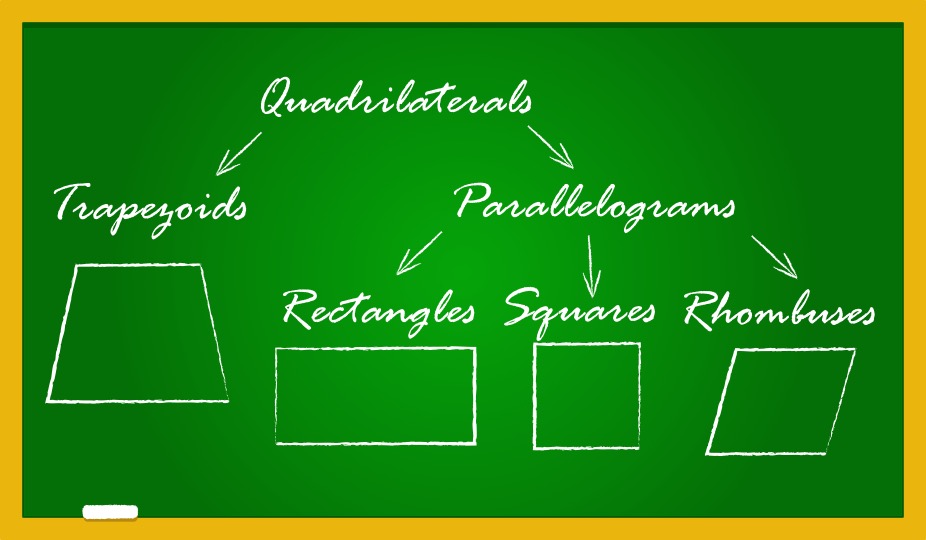
Types of Quadrilaterals and Their Properties: The Complete Family Tree

How Many Quadrilaterals Are There? Understanding the Classification

Quadrilaterals first branch into two main categories based on their shape:

Convex Quadrilaterals:

• All interior angles are less than 180 degrees
• Any line segment connecting two points within the shape lies entirely within the shape
• These appear most frequently on the GMAT
• Examples include rectangles, squares, parallelograms, and trapezoids

Non-convex (Concave) Quadrilaterals:

• At least one interior angle is greater than 180 degrees
• Some line segments drawn between points within the shape will pass outside the shape
• Often have a portion that “caves in” (resembling arrowheads or bowties)
• Less frequently tested on the GMAT but may appear in more advanced questions

The Hierarchical Relationship Between Quadrilateral Types

From here, we can further classify the convex quadrilaterals that you’ll most commonly encounter on test day:

Trapezoid:

• Has exactly one pair of parallel sides (called bases)
• The non-parallel sides are called legs
• Area = (1/2) × height × (sum of parallel sides)
• An isosceles trapezoid has legs of equal length and equal base angles

Kite:

• Has two pairs of adjacent sides of equal length
• The diagonals intersect at right angles
• One diagonal bisects the other
• Has one axis of symmetry
• Area = (1/2) × product of diagonals

Parallelogram:

• Both pairs of opposite sides are parallel and equal in length
• Opposite angles are equal
• Consecutive angles are supplementary (sum to 180°)
• Diagonals bisect each other
• Area = base × height

Rectangle:

• A parallelogram with all angles equal to 90 degrees
• Diagonals are equal in length and bisect each other
• Area = length × width

Rhombus:

• A parallelogram with all sides of equal length
• Diagonals bisect each other at 90 degrees
• Area = (1/2) × product of diagonals

Square:

• A rectangle with all sides of equal length
• A rhombus with all angles equal to 90 degrees
• All sides equal, all angles 90 degrees
• Diagonals are equal, bisect each other at 90 degrees
• Area = side² or (diagonal)²/2

GMAT Tip: When you see a square in a problem, remember it inherits ALL properties of both rectangles AND rhombuses. This dual inheritance is frequently tested!

Quadrilateral Properties Chart: Quick Reference Guide

The following table summarizes the key properties of common quadrilaterals. Notice how properties cascade down through the hierarchy:

Properties of quadrilaterals	Rectangle	Square	Parallelogram	Rhombus	Trapezium
All Sides are equal	No	Yes	No	Yes	No
Opposite Sides are equal	Yes	Yes	Yes	Yes	No
Opposite Sides are parallel	Yes	Yes	Yes	Yes	Yes
All angles are equal	Yes	Yes	No	No	No
Opposite angles are equal	Yes	Yes	Yes	Yes	No
Sum of two adjacent angles is 180	Yes	Yes	Yes	Yes	No
Bisect each other	Yes	Yes	Yes	Yes	No
Bisect perpendicularly	No	Yes	No	Yes	No

Here are questions which will teach you how to apply the properties of all 5 quadrilaterals you’ll learn in this article.

Common Misconceptions About Quadrilateral Properties

Many GMAT test-takers fall into these common traps. Make sure you understand these distinctions clearly:

Misconception	Correction
“A square is not a rectangle.”	A square is absolutely a rectangle—specifically, it’s a rectangle with all sides equal.
“A rhombus is just a tilted square.”	A rhombus has all sides equal but doesn’t necessarily have 90-degree angles. A square is a special case of a rhombus.
“Trapezoids have exactly two parallel sides.”	In standard GMAT terminology, a trapezoid has exactly one pair of parallel sides. (Note: Some textbooks define trapezoids as having at least one pair of parallel sides, which would include parallelograms.)
“All quadrilaterals with perpendicular diagonals are rhombuses.”	Kites also have perpendicular diagonals but aren’t necessarily rhombuses.
“Rectangles and rhombuses are completely separate categories.”	They overlap at squares, which have properties of both shapes.

Understanding these relationships gives you a significant advantage on the GMAT. When a question mentions a square, you can immediately apply all the properties of rectangles and rhombuses to solve the problem efficiently.

Properties of Specific Quadrilaterals: A Comprehensive Guide

Properties of Parallelogram: The Foundation Shape

A parallelogram forms the foundation of the quadrilateral family hierarchy. Its properties provide the basis for more specialized shapes like rectangles and rhombuses. Understanding parallelogram properties is essential because they’re inherited by squares, rectangles, and rhombuses.

Key properties of parallelograms include:

• Opposite sides are parallel and equal in length
• Opposite angles are equal
• Adjacent angles are supplementary (sum to 180°)
• Diagonals bisect each other (cut each other in half)
• Area = base × height (perpendicular height, not side length)

These practice questions will help you solidify the properties of parallelogram

Properties of Rectangle: Right Angles and Equal Diagonals

A rectangle is a specialized parallelogram with all right angles. The properties of rectangles build upon parallelogram properties with additional features that make calculations more straightforward.

Key properties of rectangles include:

• All angles are 90° (right angles)
• Opposite sides are equal and parallel
• Diagonals are equal in length and bisect each other
• Diagonal length = √(length² + width²) (Pythagorean theorem)
• Area = length × width

These practice questions will help you solidify the properties of rectangles

Properties of Rhombus: Equal Sides and Perpendicular Diagonals

A rhombus is a parallelogram with all sides equal. The properties of a rhombus make it particularly useful for certain GMAT questions, especially those involving area calculations with diagonal measurements.

Key properties of rhombuses include:

• All four sides are equal in length
• Opposite sides are parallel
• Opposite angles are equal
• Diagonals bisect each other at right angles (perpendicular)
• Diagonals bisect the angles at the vertices
• Area = (d₁ × d₂)/2 (half the product of the diagonals)

These practice questions will help you solidify the properties of rhombus

Properties of Square: Where Rectangle Meets Rhombus

A square is a rectangle and a rhombus simultaneously. This means a square inherits all the properties of both shapes, making it the most specialized quadrilateral with the most defined properties.

Key properties of squares include:

• All four sides are equal in length
• All four angles are 90° (right angles)
• Opposite sides are parallel
• Diagonals are equal in length, bisect each other, and are perpendicular
• Diagonal length = side length × √2
• Area = side² or (diagonal)²/4

These practice questions will help you solidify the properties of squares

Properties of Trapezium (Trapezoid): The Single Parallel Pair

A trapezoid (also called trapezium in some countries) has exactly one pair of parallel sides, making it distinct from the parallelogram family. The properties of trapezoids are frequently tested on the GMAT, especially in area calculations.

Key properties of trapezoids include:

• Exactly one pair of parallel sides (the bases)
• The non-parallel sides are called legs
• In an isosceles trapezoid, the legs are equal in length
• The midsegment (line connecting midpoints of non-parallel sides) is parallel to the bases and equal to their average
• Area = (1/2) × height × (sum of parallel sides)

Properties of Kite Quadrilateral: Adjacent Equal Sides

A kite has two pairs of adjacent equal sides, creating a distinctive shape with unique properties. Understanding kite properties helps solve specific types of GMAT problems, particularly those involving diagonals and area.

Key properties of kite quadrilaterals include:

• Two pairs of adjacent sides are equal in length
• One diagonal bisects the other diagonal
• Diagonals intersect at right angles (perpendicular)
• The diagonal that bisects the other diagonal also bisects the angles at the vertices it connects
• Area = (d₁ × d₂)/2 (half the product of the diagonals)

Begin your GMAT preparation with the only prep company that has delivered more than 700+ scores than any other GMAT club partner. Achieve GMAT 740+ with our AI-driven tools that you personalized feedback at every step of your GMAT journey. Take our free trial today!

Did you know e-GMATers have reported more 700+ scores than ever before in GMAT Club’s history? Watch this video to understand how e-GMAT has achieved this record-shattering result by investing and innovating with a single goal in mind – To create a platform that empowers students to achieve and deliver their very best.

Quadrilateral Hierarchy: “Always, Sometimes, Never” Relationships

Is a Rectangle a Parallelogram? Understanding Subset Relationships

Understanding hierarchical relationships between quadrilaterals is critical for GMAT success. A rectangle is always a parallelogram, but a parallelogram is only sometimes a rectangle (when all angles are 90°). Similarly, is a square a parallelogram? Yes, always—because a square inherits all parallelogram properties.

This hierarchical understanding helps you answer “always, sometimes, never” questions correctly and apply the right properties to each shape.

Property Inheritance in the Quadrilateral Family

Understanding property inheritance is crucial for efficient problem-solving:

• Inheritance Principle: A specialized shape inherits all the properties of its more general “parent” shapes. Example: A square has all the properties of a rhombus (equal sides, perpendicular diagonals) AND all the properties of a rectangle (90° angles, equal diagonals).
• Property Flow: Properties flow down from general to specific shapes, not up. Example: All rectangles have equal diagonals, but not all parallelograms have equal diagonals.
• Multiple Inheritance: Some shapes inherit properties from multiple branches. Example: A square inherits from both the rectangle branch and the rhombus branch of the parallelogram family.

“Understanding that a square is always a rectangle, but a rectangle is only sometimes a square is the kind of precise thinking that the GMAT rewards.”

Test Your Understanding of Quadrilateral Relationships

Is a rectangle always, sometimes, or never a square?
Answer: Sometimes
Explanation: A rectangle is a square if and only if all its sides are equal. Many rectangles have unequal adjacent sides.

Is a rhombus always, sometimes, or never a parallelogram?
Answer: Always
Explanation: By definition, a rhombus is a parallelogram with four equal sides. It inherits all parallelogram properties.

Is a square always, sometimes, or never a rhombus?
Answer: Always
Explanation: A square is a rhombus with the additional property that all angles are 90°. Every square has four equal sides, which is the defining property of a rhombus.

Is a trapezoid always, sometimes, or never a parallelogram?
Answer: Never
Explanation: Using the exclusive definition (common on the GMAT), a trapezoid has exactly one pair of parallel sides, while a parallelogram has two pairs of parallel sides.

Is a kite always, sometimes, or never a rhombus?
Answer: Sometimes
Explanation: A kite is a rhombus if and only if all four sides are equal. Most kites have two pairs of equal adjacent sides, but not all four sides are equal.

Is a parallelogram always, sometimes, or never a rectangle?
Answer: Sometimes
Explanation: A parallelogram is a rectangle if and only if all angles are 90°. Many parallelograms have angles that are not right angles.

Is a quadrilateral with four equal sides always, sometimes, or never a rhombus?
Answer: Always
Explanation: By definition, a rhombus is a quadrilateral with four equal sides. This is the defining property of a rhombus.

Is a quadrilateral with perpendicular diagonals always, sometimes, or never a kite?
Answer: Sometimes
Explanation: Both kites and rhombuses have perpendicular diagonals, but there are other quadrilaterals with perpendicular diagonals that are neither kites nor rhombuses.

Scoring a Q50-51 on the GMAT helps you get a 700+ GMAT score. Start your journey of getting a Q50-51 on the GMAT with e-GMAT’s AI-driven online preparation course. Our xPERT not only curates the most optimized learning path but also tracks your improvement, ensuring that you get to your target Quant score quickly and reliably. Watch this video to know more:

Essential Quadrilateral Formulas for GMAT Success

When approaching quadrilateral problems on the GMAT, start by identifying exactly what you need to calculate (area, perimeter, diagonal, etc.) and what information you have available. This decision-making process will guide you to the appropriate formula.

Quadrilateral Formula Selection: Choosing the Right Approach

For area calculations, remember these key approaches:

• Square: If you know the side length s, use Area = s²
• Rectangle: With length l and width w, use Area = l × w
• Parallelogram: Use Area = b × h (base × height), not the product of adjacent sides
• Rhombus: If you know the diagonals d₁ and d₂, Area = (d₁ × d₂)/2 is often easier than using side length and angle
• Trapezoid: With parallel sides a and c, and height h, use Area = (a + c) × h/2
• Kite: With diagonals d₁ and d₂, use Area = (d₁ × d₂)/2

For perimeter calculations:

• For any quadrilateral: Perimeter = sum of all sides
• For squares and rhombuses: Perimeter = 4s (where s is the side length)
• For rectangles: Perimeter = 2(l + w)
• For parallelograms: Perimeter = 2(a + b), where a and b are adjacent sides

For diagonal calculations:

• Square: Diagonal = s√2
• Rectangle: Diagonal = √(l² + w²)
• For other quadrilaterals, diagonals may require specific properties or the application of coordinate geometry

Take a free GMAT mock to understand your baseline score and start your GMAT prep with our free trial. We are the most reviewed online GMAT Prep company with 2600+ reviews on GMATClub.

Strategic Application of Quadrilateral Formulas on the GMAT

When applying quadrilateral formulas on the GMAT, consider these strategic approaches:

1. Area Formulas in Context
   • Squares and rectangles: Questions often require you to find the dimensions first using properties like perimeter or diagonal length
   • Parallelograms: A common mistake is using side lengths instead of height—remember area = base × height (perpendicular distance between parallel sides)
   • Rhombuses and kites: The diagonal formula Area = (d₁ × d₂)/2 is usually the most efficient approach
   • Trapezoid area: Can be thought of as the average of the parallel sides multiplied by the height
2. When You’ll Need Perimeter Calculations
   • To test your ability to identify missing sides using quadrilateral properties
   • In optimization problems (e.g., “What is the maximum area for a given perimeter?”)
   • In rate problems (e.g., “Fencing a field at $x per foot”)
   • To provide additional constraints to help determine a quadrilateral’s dimensions
3. The Strategic Importance of Diagonals
   • They offer the quickest solution path for area calculations in rhombuses and kites
   • Diagonal properties help identify quadrilateral types:
     • Equal diagonals? Think rectangle
     • Perpendicular diagonals? Consider rhombus or kite
     • Diagonals bisecting each other? Look at parallelograms
   • Diagonal-side relationships can reveal missing measurements when direct measurements aren’t provided

GMAT Quadrilateral Question Patterns and Strategies

Below are four representative GMAT-style questions that demonstrate common testing patterns. For each, we’ll analyze not just how to solve it, but the strategic thinking that leads to quick, accurate solutions.

Basic Property Application Questions

Question 1: A rhombus has diagonals of lengths 6 cm and 8 cm. What is the area of the rhombus?

A) 12 square cm
B) 24 square cm
C) 30 square cm
D) 48 square cm
E) 64 square cm

Question Type: Basic property application
Property Focus: Area of a rhombus using diagonals

Strategic Analysis: This question tests your knowledge of the formula for calculating a rhombus’s area using its diagonals. The key insight is recognizing that for a rhombus, the diagonals bisect each other at right angles, allowing use of the formula Area = (d₁ × d₂)/2.

Step-by-Step Solution:

1. Identify diagonal lengths: d₁ = 6 cm and d₂ = 8 cm
2. Apply the rhombus area formula: Area = (d₁ × d₂)/2
3. Substitute values: Area = (6 × 8)/2 = 48/2 = 24 square cm

The answer is B) 24 square cm.

Pattern Recognition Tips: When you see a rhombus with given diagonals, immediately recall the area formula using diagonals. Unlike other quadrilaterals, the rhombus area formula specifically leverages the diagonal lengths rather than side lengths.

Quadrilateral Relationship Questions

Question 2: Which of the following statements must be true for a quadrilateral with exactly one pair of parallel sides?

I. The quadrilateral is a trapezoid.
II. The sum of the angles is 360 degrees.
III. The opposite sides are of equal length.

A) I only
B) II only
C) I and II only
D) II and III only
E) I, II, and III

Question Type: Property relationship
Property Focus: Trapezoid definition, angle properties of quadrilaterals

Strategic Analysis: This question tests your understanding of trapezoid definitions and general quadrilateral properties. You need to evaluate which statements are universally true versus conditionally true.

Step-by-Step Solution:

• Statement I: A quadrilateral with exactly one pair of parallel sides is the definition of a trapezoid. TRUE.
• Statement II: All quadrilaterals have angles that sum to 360 degrees. This is a fundamental property of all quadrilaterals. TRUE.
• Statement III: Having opposite sides of equal length is a property of parallelograms, not trapezoids. A trapezoid has only one pair of opposite sides parallel (and not necessarily equal). FALSE.

Since statements I and II must be true, the answer is C) I and II only.

Pattern Recognition Tips: Property relationship questions typically ask which properties always hold true for a specific quadrilateral type. Remember the hierarchical relationships between quadrilaterals and their defining vs. resulting properties. 

Data Sufficiency Quadrilateral Questions

Question 3: Is quadrilateral ABCD a rhombus?

(1) All sides of quadrilateral ABCD are equal in length.
(2) The diagonals of quadrilateral ABCD bisect each other.

A) Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
B) Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
C) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
D) EACH statement ALONE is sufficient.
E) Statements (1) and (2) TOGETHER are NOT sufficient.

Question Type: Data sufficiency
Property Focus: Defining properties of rhombuses vs. other quadrilaterals

Strategic Analysis: This question tests your knowledge of the minimum conditions needed to define a rhombus. Success requires understanding which properties are necessary versus sufficient for identifying a rhombus.

Step-by-Step Solution:

Statement (1): All sides of quadrilateral ABCD are equal in length.

• This could describe a rhombus or a square (which is also a rhombus)
• However, not all quadrilaterals with equal sides are rhombuses (consider an equilateral quadrilateral with non-bisecting diagonals)
• NOT SUFFICIENT

Statement (2): The diagonals of quadrilateral ABCD bisect each other.

• This is a property of all parallelograms (rhombuses, rectangles, squares)
• Without information about the sides, we can’t determine if it’s specifically a rhombus
• NOT SUFFICIENT

Statements (1) and (2) together:

• Equal sides (from statement 1)
• Diagonals that bisect each other (from statement 2)
• These two properties together uniquely define a rhombus
• SUFFICIENT

The answer is C) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.

Pattern Recognition Tips: For data sufficiency geometry questions, focus on the minimum conditions needed to uniquely identify a figure. Property combinations often provide sufficiency where individual properties fail. 

Area/Perimeter Optimization Problems with Quadrilaterals

Question 4: A farmer wants to enclose a rectangular field with 100 meters of fencing. What are the dimensions of the field that will maximize the enclosed area?

A) 20 meters by 30 meters
B) 25 meters by 25 meters
C) 40 meters by 10 meters
D) 45 meters by 5 meters
E) 50 meters by 0 meters

Question Type: Optimization problem
Property Focus: Relationship between perimeter and area

Strategic Analysis: This question tests understanding of the relationship between a rectangle’s perimeter and area. The key insight is recognizing that for a fixed perimeter, a square yields the maximum possible area among all rectangles.

Step-by-Step Solution:

1. Let length = l and width = w
2. From the perimeter constraint: 2l + 2w = 100
3. Solving for one variable: l = (100 – 2w)/2 = 50 – w
4. The area function: A = l × w = (50 – w) × w = 50w – w²
5. To maximize area, find where dA/dw = 0: dA/dw = 50 – 2w = 0 → w = 25
6. Using w = 25, we get l = 50 – 25 = 25
7. The dimensions are 25 meters by 25 meters (a square)

The answer is B) 25 meters by 25 meters.

Pattern Recognition Tips: For optimization problems with fixed perimeter, remember that the square always yields the maximum area. This principle appears frequently on the GMAT in various contexts. 

Watch this GMAT geometry-free webinar where we discuss how to solve 700-level Data sufficiency and Problem questions in GMAT Quadrilaterals:

Conclusion: Mastering Types of Quadrilaterals and Their Properties

The study of quadrilaterals for the GMAT isn’t about memorizing isolated facts, but understanding a clear hierarchical structure—from general quadrilaterals down to specific shapes like squares—with each shape inheriting properties from its parent categories.

Remember this key hierarchy to avoid confusion:

• All quadrilaterals have 4 sides and angles summing to 360°
• Parallelograms have opposite sides parallel and equal
• Rectangles are parallelograms with all 90° angles
• Rhombuses are parallelograms with all sides equal
• Squares are both rectangles and rhombuses (all sides equal, all angles 90°)
• Trapezoids have exactly one pair of parallel sides

The “always, sometimes, never” relationships between quadrilateral types are particularly important for answering property comparison questions quickly and accurately.

At e-GMAT, we strive to make the students’ life easier at every level and therefore, we have built this fantastic tool called the GMAT Personalized Study Planner. With this tool, you can not only find out the Quant and Verbal Sectional scores but also Sub-sectional scores in Quant (Algebra, Arithmetic, etc.) and Verbal (CR, RC, and SC) to achieve your target GMAT Score! Moreover, this tool will craft your very own study plan in 5 minutes. Register for our FREE Trial and create your personalized study plan in 5 mins!

Further reading:

• Geometry Questions – Most Common Mistakes | GMAT Quant Prep
• Circle Formulas – Area and Perimeter
• Properties of Numbers – Even & Odd | Prime | HCF & LCM
• Properties of Triangles – Definition | Types | Classification
• Lines and Angles – Properties and their Application

Are you planning to enroll at top business schools? Let us help you conquer the first step of the process i.e., taking the GMAT. Take a free GMAT mock to understand your baseline score and start your GMAT prep with our free trial. We are the most reviewed online GMAT Prep company with 2500+ reviews on GMATClub, as of January 2023.

Write to us at acethegmat@e-gmat.com in case of any query.

FAQs -Properties of Quadrilaterals