In the last article in the GMAT Geometry Series, we explained properties of different types of triangles and how those properties will help you solve GMAT geometry questions on triangles. We illustrated them with GMAT geometry practice problems and also asked you to solve some GMAT Geometry Practice Problems.

In this article, we will look at three special properties which are tested by GMAT in Geometry:
- How a median affects the area of any triangle
- Sum of External Angles of a triangle
- Angle Side Property of Right Angled Triangle
- GMAT Geometry Practice Problems with Detailed Solutions
- Takeaways & Geometry Sample Problems
If you haven’t gone through the previous articles of this series, here are the links-
Learn how a median affects the area of any triangle
Consider any triangle ABC and draw a line joining A to the midpoint of BC. Let’s call this line AD. Now tell me, what can we infer about the area of triangle ABD and ACD?
Is there any relation between them?
We know,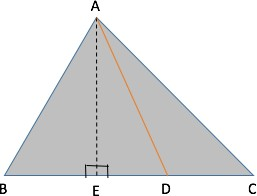
Area of a triangle = (1/2) x base x height
So, let us drop a perpendicular from A on BC and name it AE.
Since the heights of triangle ABD and ACD are equal to AE, we can write:
Area of triangle ABD = ½ x BD x AE
Area of triangle ACD = ½ x CD x AE
Also, since D is the midpoint of BC, we have CD = BD
Hence, we can conclude that:
Area of triangle ABD = Area of triangle ACD
For any strategic advice for GMAT or MBA Admissions, write to us at acethegmat@e-gmat.com. Sign up for free trial and get unlimited access to concept files, live sessions, and practice questions.
We know that the line joining a vertex of a triangle to the midpoint of the opposite side is called a median of the triangle.
Therefore, we found that the median AD divides the triangle into two equal areas.
Let us look at an Official question which can be solved very quickly, using the above property.
GMAT Quant Official Guide Question | (GMAT Data Sufficiency)
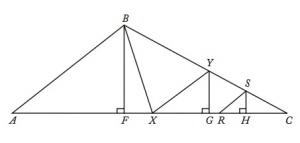
A slightly edited version of OG Question: OG 16 DS 126
In triangle ABC, point X is the midpoint of side AC and point Y is the midpoint of side BC. If point R is the midpoint of line segment XC and if point S is the midpoint of line segment YC, what is the area of triangular region RCS, if the area of triangular region ABX is 32 square units?
This diagram might look scary and the question might seem undoable at the beginning. But let us simplify the diagram, concentrating only on the medians, BX, XY, RS and RY (join RY in the diagram). In doing so, the diagram will look as follows:
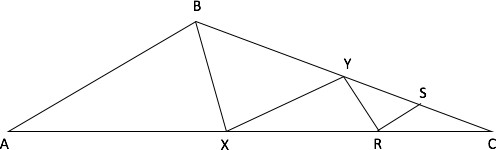
Solution:
Since BX is a median in triangle ABC, we can use the Special Property to conclude that
Area of ABX = Area of BXC
It is given that the Area of triangle ABX = 32 square units.
Hence, Area of BXC = 32 square units.
Since XY is a median in triangle BXC, we can conclude that
Area of BXY = Area of XYC = 32/2 = 16
Since RY is a median in triangle XYC, we can conclude that
Area of RYX = Area of RYC = 16/2 = 8
And since RS is a median in triangle YRC we can conclude that
Area of YRS = Area of RCS = 8/2 = 4
So, is this question really tough? Definitely, not as tough as it looked at the beginning.
We used one simple and special property to elegantly solve a complicated looking question.
Discover the Property of Sum of External Angles of a triangle
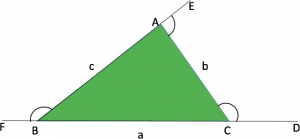
We know that,
An external angle = sum of two opposite interior angles
In the above diagram,
ABC is a triangle with sides extended as shown.
Therefore, using the above property we can write,
Ext. ∠ ACD = int. ∠CAB + int. ∠CBA
But hold on, that is not the special property!
Now you know that the sum of internal angles = 180°.
But what about the sum of external angles?
If we add up all the external angles as shown in the diagram, we will get
Ext ∠ (ACD + CAE + ABF) = int. ∠ (2A + 2B + 2C) = 2 x 180° = 360°
Hence, the sum of external angles = 360°
We will discuss this property in more details for Polygons, where I will show you that sum of external angles is equal to 360° for any convex polygon, irrespective of the number of sides the polygon has.
A Cheeky Trick on Angle-Side Property of Right Angled Triangle
While going through GMAT geometry practice problems on right-angled triangles, the most commonly tested right-angled triangles are ones with the following set of values as its angles.
- 30° – 60° – 90°
or
- 45° – 45° – 90°
Therefore, it is important for us to know the relation between these angles and the sides of the triangles, as knowing this can help us in finding the answer quickly and at the same make the calculations significantly simple.
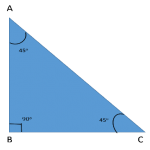
Case 1:
As shown in the figure, if the angles of the triangle are 30°-60°-90°, the ratio of the sides will be –
AB: BC: AC = 1: √3: 2
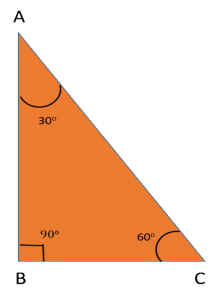
Case 2:
As shown in the figure, if the angles of the triangle are 45°-45°-90°, the ratio of the sides will be –
AB: BC: AC = 1: 1: √2
Application of Sum of External Angles and Right Angle
Let us apply the special property 2 and 3 in a very simple GMAT-like question.
The two questions given below are based on the same diagram, so let’s solve these questions together to understand the application of the above properties.
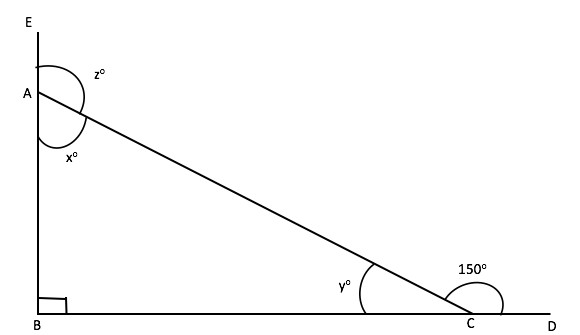
Q.1 What is the value of z?
- 110°
- 120°
- 130°
- 140°
- 150°
Q.2 If the value of AC = 4 units, what is the ratio of the sides AB and BC?
- 2 : 1
- 1 : √ 3
- 2 : √ 3
- √ 3 : 1
- 1 : 2
Detailed Solution to the above GMAT Geometry Practice Problem:
Part 1:
Notice carefully, that z is the external angle of triangle ABC.
From our conceptual understanding related to angles of a triangle, we can write –
External ∠CAE = sum of opposite internal angles of triangle ABC
Therefore, ∠z = ∠ABC + ∠ACB
From the diagram, we can clearly infer that –
∠ABC = 90° and ∠ACB = y°
Also, ∠ACB + ∠ACD = 180° [straight line angle property] And, ∠ACD = 150°
Therefore, ∠ACB = 180° – 150° = 30°
Hence, the value of ∠z = ∠ABC + ∠ACB = 90° + 30° = 120°
Part 2:
This question can be solved in multiple ways –
Method I:
We know that
- AC = 4 units
and
- from our above discussion in part 1 we know that ∠ACB = 30°
Therefore,
length AB = AC sin 30° = 4 x ½ = 2
And BC = AC cos 30° = 4 x √3/2 = 2√3
Therefore, ratio of AB : BC = 2 : 2√3 = 1 : √3
Method II:
But say one does not know trigonometry but still wants to solve it. This is where, our
Special Property 3, Case 1 comes in handy!
- If we observe carefully, we will notice that triangle ABC is a 30°-60°-90° triangle
- Since ∠ABC = 90° , ∠BAC = 60° and ∠ACB = 30°
- And we know that ratio of AB : BC : CA = 1 : √3 : 2
Therefore, from here, we can directly say that the answer would be 1 : √3 and we don’t even have to use the value of AC to find the answer!
Cool, isn’t it?
GMAT Geometry Practice Problems – Another Question to test your imagination
A 60 feet long ladder is inclined against a wall such that the bottom and the top of the ladder are at equal distance from the point where the wall meets the floor. The same ladder slides away from the foot of the wall such that it is inclined at an angle of 30° from the floor. What is the difference between the heights to which the ladder reaches in the two cases?
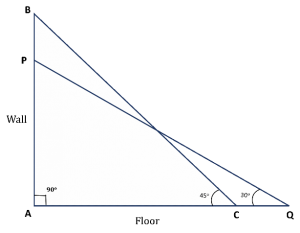
- 15(√ 2 – 1)
- 30(√ 2 – 1)
- 15(√ 2 + 1)
- 30√ 2
- 30(√ 2 + 1)
Solution:
Approach
Now this question might seem to be a tough one because the position of the ladder is different in the two cases, which leads to change in the angles with respect to the floor. Therefore, most students might feel that this question might not be an easy one to solve.
But no need to worry, let’s see how by using our special property and a methodical approach, we can get our answer very easily!
Step 1: Drawing Inferences from the Question Statement
Let us represent the two cases diagrammatically.
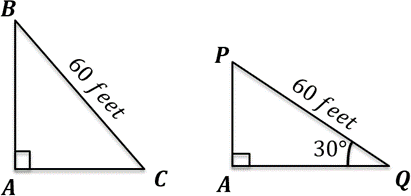
Triangle BAC represents the initial case, where point A is the point of intersection of the wall and the floor and BC represents the ladder.
We are given that AB = AC and BC = 60 feet.
Triangle PAQ represents the case after the ladder slid. The only value that remains unchanged is the length of the ladder, hence BC = PQ.
Therefore, in the Right Triangle PAQ,
PQ = 60 feet, and ∠AQP = 30°
We need to find the value of AB – AP.
Step 2: Finding the required values
Let us first consider Right Triangle BAC:
We know that when two sides of a right triangle are equal, it is a 45°-45°-90° triangle.
As discussed in special property 3, in such a triangle, the sides opposite to the angles 45°, 45°, and 90° respectively are in the ratio 1: 1: √2
Therefore,
![]() ⟹
⟹ ![]()
Thus, we have found out the value of AB.
Now, considering Right Triangle PAQ:
It is a 30°-60°-90° right-angled triangle. And we know that in such a triangle, the sides opposite to the angles 30°, 60°, and 90° respectively are in the ratio 1 : √3 : 2.
Therefore,
![]()
⟹ ![]()
Step 3: Calculate the final answer
Difference between the heights to which the ladder reaches in the two cases
= AB – AP
= 30√2 – 30
= 30(√2 – 1)
Answer: Option (2)
Takeaways & GMAT Sample Problems
Any geometry question testing the concepts of triangles can be easily tackled as long as the test taker is clear with:
- the basic properties of a triangle
- the subtle differences these properties exhibit, depending on the type of the triangle
- when to apply and how to apply these (Focus on the questions that are given in the article and understand how each of these properties is used in each question)
Access our Next Series of articles on Number Properties!
With this, we come to the end of our series on GMAT Geometry. We hope you liked our articles as much as we liked creating them. Remember the takeaways from our articles on GMAT Geometry and go through GMAT geometry sample problems and geometry practice problems.












