In the last article, we explained: “Why GMAT Geometry is a weak area” for most students and how you can improve it. We explained various concepts of triangles and their application in GMAT like questions through various illustrative examples. As a continuation, this article covers the different types of triangles and their properties. We have also included some geometry practice questions at the end of the article. Here is how the article has been structured:
- Properties of different types of triangles
- Takeaways & Illustrative Examples
- Geometry Practice Questions
If you haven’t gone through the previous articles of this series, please browse through the following links:
- Most common mistakes in GMAT Geometry Questions
- GMAT Geometry formulas and concepts on Triangles- Part 1 (covers the following)
- Identifying whether a set of given numbers could be the lengths of the three sides of a triangle
- Range of possible values of the length of one side of a triangle given the lengths of the other two sides
- Various properties of the angles of the triangle.
Check out the next article in the series: Geometry Practice Problems and Special Properties of Triangles (Part 3)
With the above knowledge in mind, let us now look at the different types of triangles and how their properties differ from one another. Then we will apply the learnings to two GMAT like questions.
Feel free to write to us at acethegmat@e-gmat.com in case you have any query.
Properties of different types of triangles tested in GMAT Geometry
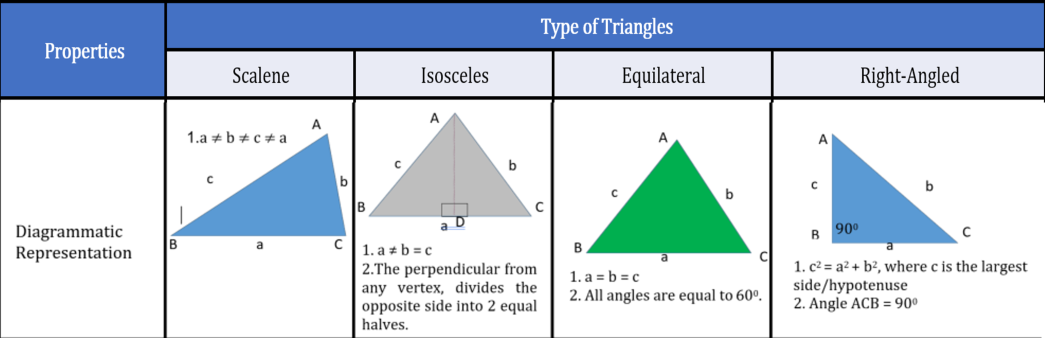
The table given below lists down the various types of triangles and their properties that are tested on the GMAT. The triangles are sequenced in such a way that the transitions/subtle differences in the corresponding properties are clearly visible.
|
Properties | Type of Triangles | |||
| Scalene | Isosceles | Equilateral | Right-Angled | |
|
Side Property | • None of the sides are equal
• a ≠ b ≠ c ≠ a where a, b and c are three sides of the triangle |
• Two sides are equal. • a ≠ b = c, where a, b and c are the three sides of the triangle |
• All the sides are equal • a = b = c, where a, b and c are the three sides of the triangle. | • Two sides forming the right angle may or may not be equal
• If they are equal, the triangle is known as an isosceles right-angled triangle |
|
Angle Property | • All the angles are distinct | • Angles opposite to equal sides are equal. | • All angles are equal to 60º | • One of the angles is 90º |
|
Area Formula |
• Area = ½ x base x height •The above formula is applicable to triangles | • Area = √3/4 x a²,
where ‘a’ is the length of a side of the triangle |
• Area = (½) x base x perpendicular | |
|
Special Property | • The perpendicular drawn to the unequal side divides it into two equal parts. | • The perpendicular from any vertex divides the opposite side into 2 equal halves. |
• According to Pythagoras Theorem, c²= a² + b², where c is the largest side/hypotenuse |
Diagrammatic Representation:
Let us walk you through the content of the table one by one and look at the subtle differences that should be kept in mind while solving any GMAT geometry problems on triangles.
1. Side Property
- None of the sides of a scalene triangle is equal
- Any two sides of an isosceles triangle are equal
- All the sides of an equilateral triangle are equal
Note: A right-angled triangle can be a scalene triangle or an isosceles triangle. It depends on whether the lengths of the perpendicular and the base are equal.
Can you tell why can’t a right-angled triangle be an equilateral triangle?
2. Angle Property
- None of the angles of a scalene triangle is equal.
- The two angles opposite the two equal sides of an isosceles triangle are equal
- All the angles of an equilateral triangle are equal
Can you notice the relation between the sides and the angles?
- In a scalene triangle where none of the sides are equal, no two angles are equal
- In an isosceles triangle where two sides are equal, the angles opposite to the equal sides are equal.
- In an equilateral triangle where all sides are equal, all angles are equal to 60º.
Note: A right-angled triangle has one of its angles as 90º. Since it can be a scalene triangle or an isosceles triangle, the value of the other two angles will depend on what kind of triangle it is.
3. Area Property | (with Geometry Practice Questions)
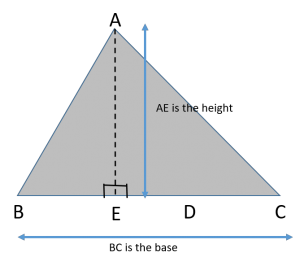
The area of any triangle can be found using the formula – Area = ½ x base x height
For an Equilateral triangle we sometimes use the formula given below to calculate the area quickly: (Note that in an Equilateral triangle, all sides and angles are equal)
Area = (√3/4) * a²
Where ‘a’ is the length of each side of the triangle.
Note: The area of an equilateral triangle or any special triangle is derived from the basic formula –
Area = ½ x base x height
Thus, if we remember this formula, it is more than enough to solve any problem related to finding the area of a triangle.
4. Special Property of Triangles | (Geometry Practice Questions included below)
Isosceles Triangle
The line joining one vertex of a triangle to the midpoint of the opposite side is called a median of the triangle. In the case of an isosceles triangle, the median and the perpendicular is the same, when drawn from the vertex which joins the two equal sides.
Hence, from the given diagram, we can say that line AD acts as a median, dividing the base BC into two equal halves, and that AD is also perpendicular to BC
Right Angled Triangle
The Right-Angled Triangle has three sides known as the perpendicular, base, and hypotenuse. The hypotenuse is the largest side and the angle opposite to it is the largest angle and measures 90º. We can apply Pythagoras Theorem, to define the relationship between perpendicular, base, and hypotenuse.
From the given diagram, we can write:
(Hypotenuse)² = (perpendicular)² + (base)²
AC² = AB² + BC²
Let us now understand how to apply the above-mentioned properties with the help of two GMAT like geometry practice questions.
Illustrative Example 1 | Geometry Practice Questions

In triangle ABC, is AC² = AB² + BC²?
- ∠BAC + ∠ACB = ∠ABC
- AB = BC
Explanation:
Steps 1 & 2: Understand Question and Draw Inferences
To find: Is AC² = AB² + BC²?
Using Pythagoras theorem, we know that the above is true if ∠ABC=90º
Because we can apply the property that we have learned from the table given above that AC² = AB² + BC² only when ABC is a right-angled triangle.
Step 3: Analyze Statement 1 independently
Statement 1 tells us that ∠BAC + ∠ACB = ∠ABC
Using Angle Sum Property in triangle ABC, we can write:
∠BAC+∠ACB+∠ABC=180º
Substituting the value of ∠BAC + ∠ACB from Statement 1, we have
∠ABC+∠ABC =180º
2(∠ABC) = 180º
Therefore, ∠ABC=90º
Since we could find a unique answer to the question, Statement 1 alone is sufficient.
Step 4: Analyze Statement 2 independently
Statement 2 tells us that AB = BC
Using the table given above, we can see that this is a property of an isosceles triangle.
Thus, triangle ABC is an isosceles triangle.
However, we cannot conclude that ABC is a right-angled triangle because not every isosceles triangle is right-angled.
Hence, this statement is clearly not sufficient to solve the question. Therefore, Statement 2 is not sufficient.
Step 5: Analyze Both Statements Together (if needed)
Since we’ve already arrived at a unique answer in Step 3, this step is not required. Answer: Option A
Illustrative Example 2 | Geometry Practice Questions
The area of an equilateral triangle is √3 times the area of an isosceles triangle. If the three sides of the isosceles triangle are 5, 5 and 6. Find the length of each side of the equilateral triangle.
- 4
- 6
- 4√3
- 8
- 6√3
Solution: From the triangle property table, we can use two properties to solve this question.
-
Isosceles Special Property: The perpendicular drawn to the unequal side, divides the unequal side into 2 equal halves.
Let’s name the isosceles triangle as ABC, where AB = AC = 5 units and BC = 6 units.
The perpendicular from A on BC will divide BC into 2 equal halves. So, BD = DC = 3 units
Using Pythagoras Theorem, we can write AB² = AD² + BD²
⟹ 5² = AD² + 3²
Therefore, AD = 4 units.
Area of triangle ABC = ½ x AD x BC = ½ x 4 x 6 = 12 units.
-
Area of an equilateral triangle = (√3/4) x side²
Since it is given that area of equilateral triangle = √3 x area of an isosceles triangle
Therefore, (√3/4) x side² = √3 x 12
⟹ Side = 4√3
Hence, the correct answer is Option C.
If you are planning to take the GMAT, we can help you with a personalized study plan and give you access to quality online content to prepare. Write to us at acethegmat@e-gmat.com. We are the most reviewed GMAT prep company on gmatclub with more than 2400 reviews and are the only prep company that has delivered more than 700+ scores than any other GMAT club partner. Why don’t you take a free trial and judge for yourself?
Takeaways – Special Properties of Triangles
We hope these questions helped you in understanding the importance of the properties of triangles and their application in GMAT context. Try to remember these properties in a methodical manner as given in the table and we are sure that you will be able to apply them successfully in all questions related to triangles.
Keeping these takeaways in mind, can you solve the 2 questions?
GMAT Geometry Practice Questions
Make sure to present your analysis for these questions. Happy Learning!
In the next articles on Triangles, read about “Special properties of Triangles tested on the GMAT”. For further help and Geometry Practice Questions, take up our Free Trial. Feel free to write to us at acethegmat@e-gmat.com!












