A 10 min read

Are you always confused whether to add or multiply the cases while solving GMAT permutation and combination questions? Do you often get questions incorrect simply because you added entities instead of multiplying them? If the answer to any of the above questions is yes, then read further and learn how to get rid of the confusion by using “AND” & “OR” on GMAT Permutation and Combination questions.

Are you struggling with GMAT quant? e-GMAT provides structured learning from foundations to help you master the skills needed for a high score. Join the world’s most successful prep company for a free trial and see the difference it can make. We are the most reviewed online GMAT Prep company with 2500+ reviews on GMATClub, as of March 2023.

When to add – usage of the keyword “OR”- Concept 1

While solving any Permutation and Combination question in the GMAT, the most frequent confusion that students have is: “Do I need to add up all the cases or do I need to multiply all the cases?” Let’s understand what I am trying to say with the help of two questions.

• Amy has 3 different types of shoes and 2 different types of sandals. Whenever she goes out, she likes to wear either a shoe or a sandal. In how many ways can she decide what to wear?
• Joe has 3 different types of shirts and 2 different types of trousers. Whenever he goes out, he likes to wear a shirt and a trouser. In how many ways can he decide what to wear?

Look at these two situations. In both these cases, the numbers are the same. The only difference is that Amy will choose either shoes OR sandals to wear and in the second case, Joe is going to choose both a shirt AND a trouser.

Let us focus on Amy’s situation first, and then we will come to Joe.

Solution:

Assuming that she has red, green, and black shoes, and she has brown and blue sandals, let us list down all the possible options that she has.

1. She can wear Red Shoes OR
2. She can wear Green shoes OR
3. She can wear Black Shoes OR
4. She can wear Brown Sandals OR
5. She can wear Blue Sandals

Notice how we have used the word OR after every case. The OR here emphasizes the fact that Amy does not have the option to wear two different kinds of things at the same time! She needs to choose only 1 of these.

Thus, the answer, in this case, will be 5.

Now let us use the keyword approach (OR) to solve this question easily!

Save 60+ hours of GMAT preparation by crafting a well defined study plan in just 3 steps:

When to Multiply – Usage of Keyword “AND” – Concept 2

Now let us look at Joe’s case.

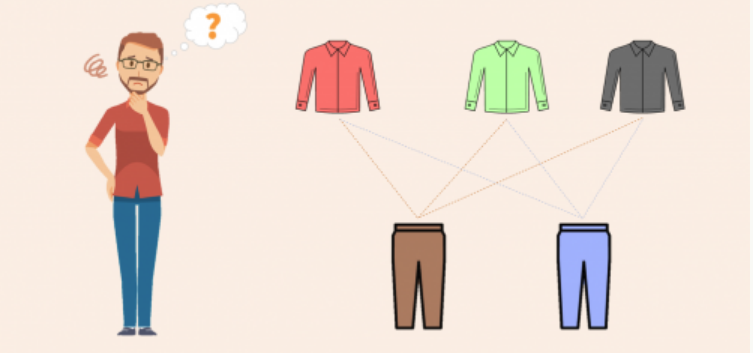
Assuming that he has red, green, and a black shirt, and he has brown and blue trousers, let us list down all the possible options that he has.

1. He can wear a Red Shirt AND Brown Trousers
2. He can wear a Red Shirt AND Blue Trousers
3. He can wear a Green shirt AND Brown Trousers
4. He can wear a Green shirt AND Blue Trousers
5. He can wear a Black Shirt AND Brown Trousers
6. He can wear a Black Shirt AND Blue Trousers

Notice how I have used the word AND after each and every case. The AND here emphasizes the fact that Joe must wear both shirt AND trousers at the same time!

We cannot imagine a scenario, where he wears just a shirt OR just a trouser.

From the above cases, we can see that he has 6 different options for wearing a shirt and a trouser.

Now let use the keyword approach (AND) to solve this question easily!

Look at the question once again:

• Joe has 3 different types of shirts and 2 different types of trousers. Whenever he goes out, he likes to wear a shirt AND a trouser. In how many ways can he decide what to wear?
  • Notice the AND that I have highlighted in this question.
• In this case, also focus on what we need to find out.
  • In this case, we need to find the number of ways he can wear a shirt AND a trouser.
  • Since the word AND is used here, we can conclude that both the events need to happen together.
• Which means he needs to wear a shirt and trousers together.

Whenever we have a situation in which two events can happen simultaneously, we simply “multiply” all the cases.

Thus, in this case, we can say:

Total possible cases for Joe = He will wear a Shirt AND he will wear Trousers

Number of ways he can wear a shirt = 3 (Red OR Green OR Black)[ Keyword OR: hence addition]

Number of ways he can wear trousers = 2 (Blue OR Brown)

Therefore, total possible cases = 3 AND 2 = 3 x 2 = 6

What to do when ‘AND’ or ‘OR’ keyword is not present?

Now, there could be a situation when the word ‘AND’ or ‘OR’ is not explicitly mentioned in the question.

What should we do then? Let us understand this with the help of 3 questions from GMAT permutation and combination:

Example 1

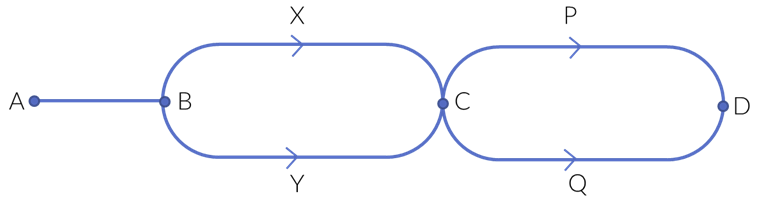
In the above diagram, in how many ways can you go from Point A to point D?

Solution

In the question and diagram, you can see that there is no mention of the word AND or OR, so what should we do?

• Well, we will simply look at the every endpoint and figure out what are we exactly doing.
• So, think, in how many ways can we go from point A to B?
  • We can go in one way, right?
  • So, let us just write A => B: 1 way
• Now, when we want to go from B to C, we can go via X OR Y.
  • Notice how we are using the word OR here.
  • We know that we cannot simultaneously go via both the routes. And thus, we need to use the word OR here.

• Thus, the total number of ways to go from B to C = 2
• B ->X ->C OR B->Y->C = 2 ways

• Lastly, we want to go to our destination D; we can go via P OR Q
  • In this case also, we are using the word OR.
  • Hence, we will simply ADD all the cases and get C->D = 2 ways.
• So, now we know that we can go from A to B in 1 way, then from B to C in 2 ways and from C to D in 2 ways.
  • Now, ask yourself, should we add these cases or multiply?
  • Can we reach from A to D by going through A to B or B to C or C to D?
    • No, we cannot, right?
    • We need to go from A to B AND then from B to C AND finally from C to D to reach our destination.

Thus, total cases possible are = 1 x 2 x 2 = 4 ways

Are you struggling with GMAT quant? e-GMAT provides structured learning from foundations to help you master the skills needed for a high score. Join the world’s most successful prep company for a free trial and see the difference it can make. We are the most reviewed online GMAT Prep company with 2500+ reviews on GMATClub, as of March 2023.

Example 2

Let us increase the difficulty a bit and figure out how to solve the following question.

How many 3 digits even numbers can be created using the digits 1,2,3, 4 and 5 without repetition of digits?

Solution

This question does not mention the keywords, ‘AND’ or ‘OR.’ Hence, we will try to figure out what the question is asking.

Any 3-digit number can be represented as:

We have to make a 3-digit number.

• Now think, can we make a three-digit number by just filling the Units place OR the tens place OR the hundreds place?
  • No, we cannot, Right?
• Thus, we have to fill the units place AND the tens place AND the hundreds place to get the three-digit number.
• Notice, we used the keyword AND here. Hence, we will multiply all the cases

We have to form a 3 digit even number.

• Hence, the units digit of the number must be even.
• Among the given digits: 1, 2, 3, 4, and 5, the units can be filled with 2 digits.
  • Either 2 OR 4.
  • Can you see the usage of the keyword OR here?
• Hence, the number of ways to fill the units place= 2

Now, we have filled the units digit to take care of the even nature of the number.

• We have 4 digits remaining – 1 even and 3 odd.
• The tens place can be filled with either 1 OR 3 OR 5 OR the remaining number between (2/4).
• Thus, total ways to fill tens place= 4 ways.

Now, we only have to fill the last digit and we have 3 digits remaining.

• Are you now able to visualize that we will use OR to select 1 among the 3 digits?
  • We can select either the 1st remaining digit OR the 2nd remaining digit OR the 3rd remaining digit
  • We used the keyword OR here. Hence, we will add the cases.

Thus, total ways to fill tens place= 3 ways.

As discussed, we need to multiply all these 3 individual cases to get the total number of ways in which the number can be formed.

Hence total ways= 3*4*2=24 ways

Example 3

Let us come to the last question of this article.

A committee of 2 members is to be formed from a panel of 4 male and 3 female members of a club. In how many ways can the committee be formed?

We can select either 2 males OR 2 females OR 1 male AND 1 female to form the committee.

Look for the keywords- AND and OR in the above statement.

Now it is easy, we know that we add the number of cases when we have an OR, and, we multiply the cases when we have an AND.

Total ways= (ways to select 2 males) + (ways to select 2 females) + (ways to select 1 male) x (ways to select 1 female)

Let us find in how many we can select 2 males, 2 females and 1 male and 1 female.

We have 4 males:

• We can select 2 males from 4 males in 4c2 ways and,
• We can select 1 male from 4 males in 4c1 ways.

We have 3 females:

• We can select 2 females in 3c2 ways and,
• We can select 1 female in 3c1 ways.

Thus, total ways= 4c2+ 3c2+ 4c1*3c1    = 6+3+4*3=21

Thus, the committee can be formed in 21 ways.

Takeaways – How to solve GMAT Permutation and Combination Questions

1. Specific keywords can be the X-factor in solving PNC questions. You can trust them, but at the same time apply common sense just to be sure you are on the right path.
2. Always try to figure out after reading the question whether the events are dependent or independent. Making this inference will help you solve the question more efficiently.
3. In a situation where OR is involved, please ADD up all the events.
4. In a situation where AND is involved, please MULTIPLY all the events.
5. Whenever the keyword is not available, always try to jot down all the events first and then decide whether you need them together or independently.

If you are planning to take the GMAT, we can help you with a personalized study plan and give you access to quality online content to prepare. Write to us at acethegmat@e-gmat.com. We are the most reviewed GMAT prep company on gmatclub with more than 2400 reviews and are the only prep company that has delivered more than 700+ scores than any other GMAT club partner. Why don’t you take a free trial and judge for yourself?

GMAT Permutation and Combination Practice Concepts & Questions

Now, let’s apply the above takeaways on a few GMAT-style questions. Click on the following links to access the questions:

1. Permutation and Combination Question 1
2. Permutation and Combination Question 2
3. Permutation and Combination Question 3
4. Permutation and Combination Question 4
5. Permutation and Combination Question 5

Planning on taking the GMAT? Try our free study resources (1700+ reviews on GMAT Club)

Top 3 Reasons – Why should you take the GMAT?- Read this article to know more.