A 12 min read

Like any GMAT Quant topic, Permutation and Combination has its own traps. Most students fall in these traps and ultimately, are not able to secure their target GMAT score. In this article, we will highlight 3 most common mistakes that students make in Permutation and Combination problems along with the ways to avoid the mistake. We will illustrate these mistakes through permutation and combination GMAT problems.

This is the third article of the ‘permutation and combination’ series. We would recommend reading the previous 2 articles to better grasp this article.

• Article 1 – When to add and multiply in Permutation and Combination questions 
• Article 2 – How to differentiate between Permutation and Combination Questions

Common Mistake Type 1 – Multiple Counting | Permutation and Combination

Let us look at a very simple example to understand a common mistake.

Q – There are 10 books on a shelf, of which 4 are paperbacks, and 6 are hardbacks. How many possible selections of 5 books from the shelf contain at least one paperback and at least one hardback? (OG question)

1. 75
2. 120
3. 210
4. 246
5. 252

 Solution

A common approach used by students:

We need to select 5 books such that there is at least one paperback book and at least one hardback book. So let us select 1 paperback and 1 hardback first. That will help us ensure that I have one book of each type. Then I will worry about selecting the extra 3 books from the remaining 8 books.

• Hence, the answer should be 4C₁ × 6C₁ × 8C₃.

This is how usually a lot of student approach this question and then wonder if this is the correct way to solve the question or not.

So, think, is this the right way to solve this question?

NO! It is not.

The answer is incorrect, and it is incorrect because we double counted some cases.

Are you struggling with GMAT quant? e-GMAT provides structured learning from foundations to help you master the skills needed for a high score. Join the world’s most successful prep company for a free trial and see the difference it can make. We are the most reviewed online GMAT Prep company with 2500+ reviews on GMATClub, as of March 2023.

What is Double Counting or Multiple Counting?

Let us take a small example to understand what double counting is.

We have 4 books of which 2 are paperbacks, A and B, and 2 are hardbacks, C and D. We have to find in how many ways we can select 3 books such that we have at least 1 paperback book and at least 1 hardback book.

 Solution

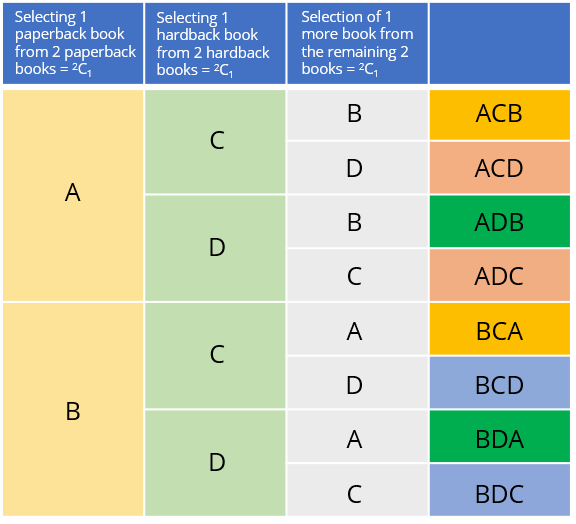
Let us list down the various combination when we solve the above example by 2C₁ × 2C₁ × 2C₁ = 8

Notice that same color-coded cells in the 4th column.

• The selection books ACB and BCA is same
• The selection books ACD and ADC is same
• The selection books ADB and BDA is same
• The selection books BCD and BDC is same

Thus, we repeated 4 cases, and that is why we were getting the wrong answer to the actual question.

We call this counting of some extra cases as double or multiple counting. 

How to avoid Double Counting in such cases? 

In questions like these, we have two categories: Hardback and Paperback. And we need a “mix” of both the types.

In scenarios like these where there are multiple categories and we need a mix of all the types, in such situations, we will first jot down all the possible cases in which all the types can be mixed or collected together.

• Thus, in this case, we will write down all the possible ways of having paperback and hardback books (keeping in mind the constraint: we need at least one book of each type)
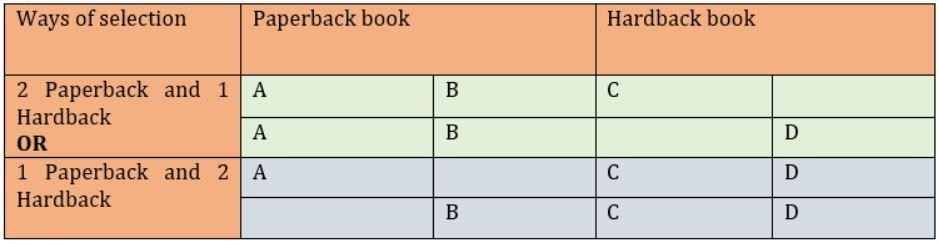
  • 3 books can be
    • 2 Paperback and 1 Hardback
    • 1 Paperback and 2 Hardback
  • Thus, Total possible ways of collecting 3 books =
    • (2 paperback AND 1 hardback) OR (1 paperback AND 2 hardback)
    • Possible way = 2C₂ × 2C₁ + 2C₁ × 2C₂ = 1 × 2 + 2 × 1= 4

Wow!!! We now know the correct approach to solve this type of question. Now here is a small exercise for you:

Let’s say you need to select 3 vehicles from 5 cars and 4 bicycles, in which we need at least 1 car and 1 bicycle. In how many ways can you do it?

Will you write it as:

• 5C₁ × 4C₁ × 7C₁ OR

Will you write is as:

• Cases Possible: 2 Cars & 1 Bicycle OR 1 Car & 2 Bicycles = 5C₂ × 4C₁ + 5C₁ × 4C₂

If you have chosen Option B. Then Congrats you have successfully learned how to avoid double counting in such cases!

Let us now solve our actual question again.

Q – There are 10 books on a shelf, of which 4 are paperbacks and 6 are hardbacks. How many possible selections of 5 books from the shelf contain at least one paperback and at least one hardback? (OG question)

1. 75
2. 120
3. 210
4. 246
5. 252 

Solution:

A common approach used by students:

We need to select 5 books such that there is at least one paperback book and at least one hardback book.

We can select 5 books in various ways:

• 1 Paperback book and 4 hardback books OR,
• 2 Paperback books and 3 hardback books OR,
• 3 Paperback books and 2 hardback books OR,
• 4 Paperback books and 1 hardback book

Let us see another case where most of the students apply double counting: The case when certain objects are identical.

GMAT geometry giving you a hard time? Read our articles on GMAT Geometry

Why don’t you try our free preparation resources? Sign up for a free trial and let us know what you think.

Common Mistake Type 2 – Identical Objects | Permutation and Combination

While solving Permutation and Combination questions, we may come across a few questions where we might be asked to select and arrange a few objects which are identical in nature.

For example, you might be asked to arrange 5 identical books, or you might be asked to arrange the word “MISSISSIPPI,” in which there are few letters which are identical (the letters I, S and P are present in this word multiple times).

Students have the tendency to make a mistake whenever they come across such cases. And thus, we should learn the best and fool-proof way to solve such questions!

Let us understand how to tackle these situations with the help of an example.

 Assume a scenario where we have 3 different letters- A, B, C and we need to form 3 letter words.

Total 3 different letter words = 3! = 6 words And these are the following cases:

• ABC
• ACB
• BAC
• BCA
• CAB
• CBA

Now, let’s play with these words!

Tell, me how many unique words will we get if we replace C by A?? If we replace C with A in the above example, we will get:

Total words = ABA + AAB + BAA + BAA + AAB + ABA = 2AAB + ABA + BAA = 2! (AAB + ABA + BAA) = 2! × 3

Now, notice that there are only 3 unique words possible: AAB, ABA and BAA. However, we have 2! multiplied with it in above equation.

Now, what should we do to get the actual answer which is 3?

• We are getting multiple cases, because we wrote AAB twice, ABA twice and BBA
• And we wrote them twice because while jotting the cases, we arrange AA in AAB, ABA and BBA twice or 2! times
• Thus, to get the actual answer, we need to divide 2! × 3 by 2!
• AAB + ABA + BAA = 6/2! = (total ways when all the letters were different)/(repetitive counting of the identical letters)

Now, let us extend this idea further to find the number of different words by using three A’s, two B’s. Since we know that we will again get repetitive cases because of three identical A’s and two identical B’s.

• Three A give only 1 word, but we counted extra cases by assuming all three A’s to be different. Hence, we will divide by 3!
• Similarly, we counted extra cases by assuming the two B’s. Hence, we will divide by 2!

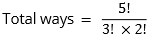
Extending the idea further, we can generalize that:

Sample Questions:

Q – In how many different ways can the letters of the word SINISTER be arranged such that two S are never together?

 Solution

SINISTER is an 8-letter word with S and I repeated two times.

We want the cases in which two S are never together and how can we do that?? We can solve the question in two ways:

• By adding all the cases when two S are separated has at least 1 letter between them
  • Ways when (Two S separated by 1 letter + Two S separated by 2 letter + ….. + Two S separated by 6 letters)
• By removing all the cases in which Two S are together from the total
  • Total cases – Number of cases in which both the S are together.

It is very clear that 2nd method is easy. Thus, we only need to find:

• Total cases in which SINISTER can be arranged and,
• Number of cases in which both the S are together

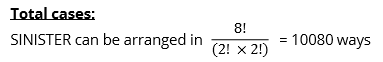
The number of cases in which both the S are together:

Two S always have to be together, so we can group together as SS. We can assume SS to be one letter as they will only be arranged like a letter with the other 6 letters.

Thus, total words = 6 letters other than S + 1 group of two S. However, SS is actually a 2-letter word which can arrange in itself.

Thus, Total ways when both the S are together = arrangement of 7 letters × arrangements in the group SS

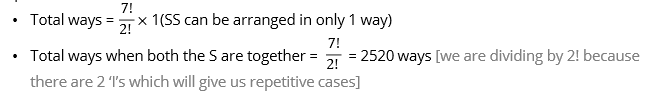
Thus, total cases in which two S are never together = 10080 – 2520 = 7560 ways.

Q – If we have 9 different points in a plane out of which 4 are collinear. How many different straight lines we can draw.

Solution

To make a straight line we need to select 2 points among 9 points. However, only 1 straight line can pass through from the 4 collinear points.

• Can you visualize that this is similar to the case of identical objects??
• In case of similar object, we only have 1 arrangement and in case of collinear points we only have 1 line.

In this case, all the lines are not repeating, only the lines whose both the points lies on 4 collinear points are repeating. Thus, we can get the line in 3 different ways:

• Select any two points from 5 non-collinear points Or,
• Select one points from 5 non-collinear points and another from 4 collinear points Or,
• 1 line from the 4 collinear points

Total ways = 5C₂ + 5C₁ × 4C₁ + 1 = 10 + 20 + 1 = 31

Thus, we will get 31 different straight lines.

Let us now move to the 3rd and one of most common type of mistake.

3 reasons why you may not achieve your target GMAT Verbal Score

Are you struggling with GMAT quant? e-GMAT provides structured learning from foundations to help you master the skills needed for a high score. Join the world’s most successful prep company for a free trial and see the difference it can make. We are the most reviewed online GMAT Prep company with 2500+ reviews on GMATClub, as of March 2023.

Common Mistake Type 3- Confusion of Powers | Permutation and Combination

To understand the third type of mistake, let us try to find the answer to one simple question.

In how many ways, 3 different prizes can be distributed to 2 students where each is eligible for all the 3 prizes?

Can you find the answer to this interesting question

• Is the answer 2³ or 3²?

Solution

If your answer is 3², then you just did a very common mistake. So, we should figure out why 3² is wrong.

Let us delve into the details of the question find this.

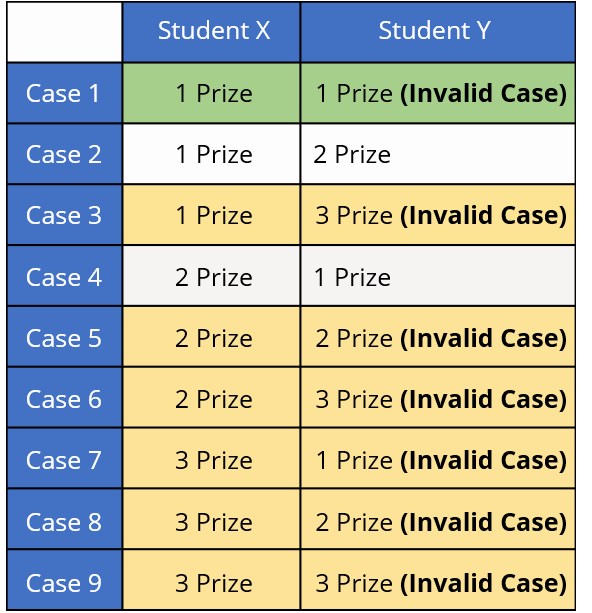
Let us suppose the two students are: X and Y, and three prizes are A, B, and C. Now, when we say that total ways to distribute the prizes = 3 × 3, we mean that:

• X can get either 1 prize or two prizes or all the three
• Similarly, Y can get either 1 prize or two prizes or all the three This can be shown in the tabular form as:

Observe Case 1:

• If, say, X gets prize A and Y gets prize B, then none of them got prize C
• There is also a possibility the both A and B might be given for the same prize A
  • Did we take any precaution that both get different prizes, while writing the first case? No, we did not.

Observe Case 3, 5, 6, 7, 8:

We are distributing more than 3 prizes to both of them, is it possible? No, right!!!! This implies that there is a mistake when we are distributing 3 prizes in 3 × 3 ways.

This is a common mistake that students make. This is known as counting invalid cases! Now, let us come to the correct approach to distribute 3 prizes in 2 students.

Correct approach

We need to distribute all the three prizes, right?

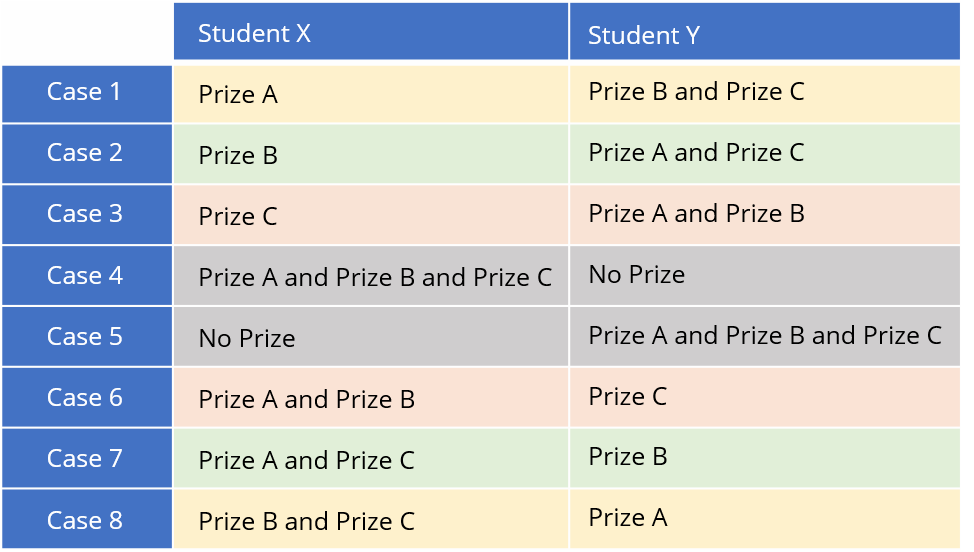
Thus, let us take Prize A and decide in how many ways can this be given to X and Y.

• Prize A can be given to either X OR Y = 2 cases
• Similarly, Prize B can be given to either X OR Y = 2 cases and
• Prize C can be given to either X OR Y = 2

Also, think, we need to distribute all the prizes, right?

• Thus, total ways to distribute prize = Give Prize A AND Give Prize B AND Give Prize C = 2 x 2 x 2 = 8 ways.

All the possible 8 cases can be shown as:

Thus, there are 2³ = 8 possible ways.

Takeaways

Solving the question in this way ensure 2 things:

1. All the prizes are distributed: A, B, and C was considered one by one and distributed.
2. Eliminates the chances of double or invalid counting, since A will go to either X or Y, similarly, B and C goes to either X or Y and not both!
3. If we replace 3 by ‘n’ and 2 by ‘r’ in the above example, then we can infer that:
   • The total number of ways to distribute ‘n- different object’in to ‘r-different things’ = rⁿ

Let us solve another example to get 100% clarity over the concept.

Q – There are 10 different envelopes and 3 post boxes. In how many ways can we post 4 envelopes in 3 post boxes such that each post box can send any number of envelopes. 

Solution

We have 10 envelopes and we need to send any 4 envelopes from 3 post-boxes.

• Thus, we first need to find select the 4 envelopes from the 10 envelopes then we can put the letter into post boxes.
  • Thus, total ways = Ways to select 4 envelopes from 10 envelopes x ways to post 4 envelopes in 4 post boxes.

Ways to select 4 envelopes

• 4 envelopes can be selected from 10 envelopes in 10C₄ = 210

Now, we have 4 selected envelopes and we need to put the selected envelopes into 3 post boxes.

Way to post 4 envelopes in 3 post boxes 

Method 1:

• Since each envelope can go into any of the post boxes thus each envelope can be posted into 3 ways
  • For example, envelope one can go in PB1 or PB2 or PB3 = 3 ways
  • And the same will be done for all the other envelopes
• Hence, total ways to post 4 envelopes in to 3 boxes = 3 x 3 x 3 x 3 = 3^4= 81

Method 2 – Use of Direct Formula:

• Here objects are envelopes and we have 4 Thus n = 4
• Since the three post boxes are the different things, in which they will be posted, r =3
• Hence, by the application of rn, total ways to post 4 envelopes into 3 boxes = 3^4 = 81 ways

Thus, total ways = 210 x 81 = 17010

Read next for our article on 3 deadly mistakes to avoid in Probability.

If you are planning to take the GMAT, we can help you with a personalized study plan and give you access to quality online content to prepare. Write to us at acethegmat@e-gmat.com. We are the most reviewed GMAT prep company on gmatclub with more than 2400 reviews and are the only prep company that has delivered more than 700+ scores than any other GMAT club partner. Why don’t you take a free trial and judge for yourself?

FAQ – Permutation and Combination