Permutations and Combinations is a topic full of conundrums. The biggest one is, understanding the difference between permutation and combination. Should I solve this question using permutation or combination? In this article, we will give you a foolproof method to differentiate between the two. In the last article of ‘Permutation and Combination’ series we talked about ‘when to ADD and MULTIPLY’?
If you haven’t read the article here is the link: GMAT Permutation and Combination | When to Add and Multiply

With the basic understanding of AND – OR keywords, let us dive into the advanced concept of the difference between permutation and combination.
- A general case on the difference between permutation and combination questions
- Keyword approach to identify combination questions
- Keyword approach to identify Permutation Questions
- Visualize difference between permutation and combination questions without keywords
- Takeaways | Difference between Permutation and Combination
Are you struggling with GMAT quant? e-GMAT provides structured learning from foundations to help you master the skills needed for a high score. Join the world’s most successful prep company for a free trial and see the difference it can make. We are the most reviewed online GMAT Prep company with 2500+ reviews on GMATClub, as of March 2023.
A general case on the difference between permutation and combination questions
In most of the permutation and combination questions, we arrive at a point where we need to select or arrange a few things and many students fall prey to the same mistake of applying selection in place of arrangement and vice-versa.
To clarify this confusion, let us discuss two simple cases:
- From 3 players, A, B, and C, how many doubles team can be formed?
- From 3 letters, A, B, and C, how many 2-digit words can be formed?

Do both the examples look the same to you?
Well, the examples are not the same.
This simple example clearly shows that the understanding of permutation and combination can help to decide when arrangement matters and when selection matters.
Keyword approach to identify combination questions
Let us understand the concept of combination by solving example 1-
Q – From 3 players, A, B, and C, how many doubles team can be formed?
Solution:
From 3 players A, B, and C, the teams of 2-players can be:
- Team AB
- Team AC
- Team BC
Thus, we can have only 3 doubles teams from 3 players.
Now, instead of solving this manually, let us apply the keyword approach to solve this question.

Important keywords to identify a combination question:
Some of the important keywords are:
- Select
- Choose
- Pick
- Combination
Whenever you read a question, look for the above keywords as these are the useful indicators that clearly tells us that the question is a combination question.
Begin your GMAT preparation with the only prep company that has delivered more than 700+ scores than any other GMAT club partner. Achieve GMAT 740+ with our AI-driven tools that you personalized feedback at every step of your GMAT journey. Take our free trial today!
Illustrative Questions:
Let us see the application of the above keywords in two GMAT permutation and combination problems.
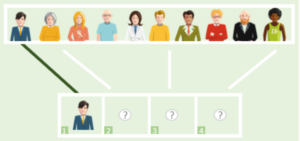
Q 1 – In a society of 10 members, we have to select a committee of 4 members. As the owner of the society, John is already a member of the committee. In how many ways the committee can be formed.
Solution
Notice the underlined keyword ‘select’ in the question.
Thus, this is a combination question. And for selection, we apply the nCr formula to arrive at the answer.
- Now, in the question, we are asked to select a committee of 4 members from 10 members and John is already a part of the committee
- Thus, we have to select 3 members among 9
- By the application of nCr formula, we can select 3 members from 9 members in 9c3 ways, which
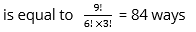
Now, let us solve a slightly difficult question.
Q 2 – An analyst will recommend a combination of 3 industrial stocks, 2 transportation stocks, and 2 utility stocks. If the analyst can choose from 5 industrial stocks, 4 transportation stocks, and 3 utility stocks, how many different combinations of 7 stocks are possible?
Solution
Notice the underlined keywords ‘Choose’ and ‘Combinations’
Now, we can easily identify that this is selection question, right?
The analyst needs to form a different combination of 7 different stocks. Can you visualize how can he do that?
Approach
- He needs to select 3 industrial stocks out of 5 industrial stock AND,
- He needs to select 2 transportation stocks out of 4 transportation stocks AND,
- He needs to select 2 utility stocks out of 3 utility stocks
- Notice the keyword ‘AND’ which indicates all the above 3 events have to occur simultaneously.
- Thus,

By the application of nCr formula, we can write:
- 3 industrial stocks out of 5 industrial stock can be selected in 5C3 = 10 ways
- 2 transportation stocks out of 4 transportation stocks can be selected in 4C2 = 6 ways
- 2 utility stocks out of 3 utility stocks can be selected in 3C2 = 3 ways
Thus, the total ways to select 7 stocks = 10 × 6 × 3 = 180 ways.
Takeaways
- Keep an eye on the important keywords like-select, choose, combination in the question stem.
- The number of ways to select ‘r’ things among ‘n’ things = nCr.
Now, let us see how permutation works.
Keyword approach to identify Permutation Questions
Let us understand the concept of permutation by solving example 2-
From 3 letters, A, B, and C, how many 2-letter words can be formed?
Solution
The 2-letter words that can be formed from 3 letters A, B, and C are:
- AB
- BA
- AC
- CA
- BC
- CB
Thus, we can form 6 different words.
Can you observe that in combination, the selection of A and B gives only 1 team i.e. AB?
However, the selection of A and B gives 2 different words i.e. AB and BA. This happens because the order of arrangement in case of words matter. But while creating teams, the team composition does not change whether we say AB or BA.
This arrangement is known as a permutation.
Can you notice the usage of keyword ‘arrangement’ in permutation?
- If not, then keep note: The word arrangement in a question implies a permutation
Now, instead of solving this manually, let us apply the keyword approach to solve this question.


Take a free GMAT mock to understand your baseline score and start your GMAT prep with our free trial. We are the most reviewed online GMAT Prep company with 2500+ reviews on GMATClub
Let us look at some frequently used keywords that imply a permutation question.
Important keywords to identify a combination question
Some of the important keywords are:
- Arrangements
- Ordered Ways
- Unique
Illustrative Questions:
Keep an eye on the above keywords in a question.
Whenever you get a question having the above three keywords, it will imply a permutation question. Let us solve 1 question to understand the application of keywords.
Q – Each signal that a certain ship can make is comprised of 3 different flags hanging vertically in a particular order. How many unique signals can be made by using 4 different flags?
Solution
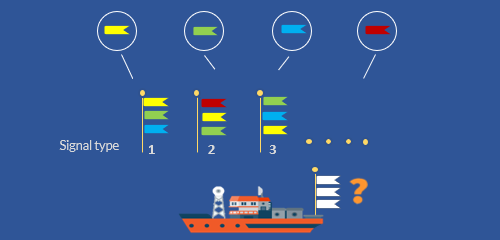

Takeaways
- Look for the important keyword-arrangements, ordered ways, and unique to identify the permutation question
- The number of ways to arrange ‘r’ things from ‘n’ things = nPr.
- An arrangement question can also be solved by first choosing ‘r’ things among ‘n’ things and then arranging all the ‘r’ things.
Scoring a Q50-51 on the GMAT helps you get a 700+ GMAT score. Start your journey of getting a Q50-51 on the GMAT with e-GMAT’s AI-driven online preparation course. Our xPERT not only curates the most optimized learning path but also tracks your improvement, ensuring that you get to your target Quant score quickly and reliably. Watch this video to know more:
Visualize difference between permutation and combination questions without keywords
At times, you can get a question that implicitly uses the application of permutation and combination. So, how do we determine whether the question is a combination question or a permutation question?
Let us understand this with the help of some examples:
Q1 – There are 8 teams in a certain league, and each team plays with the other teams exactly once. What is the total number of games played in the league?
Solution
This question does not include the important keywords then how should we solve this question?
- When we cannot find any keyword to identify whether the question is combination type or permutation type, then we need to visualize the information provided to us in the question stem.
Let us visualize the information given in the question and see if we can identify its type.
We are given:
- There are 8 teams in a league
We know that each game is played between two teams.
- The match between team A and team B is the same as the match between team B and team A
- Thus, for each match to happen, we must select 2 teams only and in this case, the arrangement will not matter
Can you observe we arrived at the keyword SELECT by dissecting the given information carefully and making meaningful inferences.
Now, we only have to find the number of ways of selecting 2 teams from 8 teams.
- Hence, total number of games played = 8C2 = 28 matches
Let us now increase the difficulty a bit and solve the next question.
Q2 – In a board meeting of the company, there are 10 members. In how ways 2 members can get the mandate for the post of CEO and COO of the company?
Solution
We do not have any keyword in the question to directly identify the type of question and apply nCr and nPr formula.
Thus, the next step to solve such type of questions is to visualize the scenario presented in the question.
- The question is about getting a mandate for the post of CEO and COO of the company
- Let us suppose A and B are the top 2 vote-getters and hence, can get the mandate for the post of either CEO or COO.
- Now, there can be 2 cases in which A and B can get the mandate
- A-> CEO and B-> COO
- B-> CEO and A-> COO

Can you see we have 2 different arrangements for the selection of 2 members only?
Thus, the arrangement after selection of 2 members implies a permutation.
Thus, we can find the answer in 2 ways:
Method 1:
By applying the formula nPr
- The number of ways in which 2 members from 10 members can get a mandate for the post of CEO and COO of the company = 10P2 = 90
Method 2:
By first selecting the 2 members from 10 members and then arranging the 2 members:
- Hence, total ways = Total ways of combination of 2 members × arranging the 2 members
- Total ways = 10C2 × r! = 45 × 2 = 90
Takeaways | Difference between Permutation and Combination
- Always keep an eye on the keywords used in the question. The keywords can help you get the answer easily.
- The keywords like-selection, choose, pick, and combination-indicates that it is a combination question.
- Keywords like-arrangement, ordered, unique- indicates that it is a permutation question.
- If keywords are not given, then visualize the scenario presented in the question and then think in terms of combination and arrangement.
Read the next article on ‘3 deadly mistakes you must avoid in Permutation and Combination‘
Are you planning to enroll at top business schools? Let us help you conquer the first step of the process i.e., taking the GMAT. Take a free GMAT mock to understand your baseline score and start your GMAT prep with our free trial. We are the most reviewed online GMAT Prep company with 2500+ reviews on GMATClub, as of January 2023.













