Ancient mathematicians introduced the concept of lines to represent straight objects which had negligible width and depth. Considered as a breadth less length by Euclid, lines form the basis of Euclidean geometry.
When two rays (part of a straight line) intersect each other in the same plane, they form an angle. The point of intersection is called a vertex.
In this article, we go over the basic properties, definitions, and types of lines and angles related to geometry. We’ll also look at a few examples for you to understand the properties of lines and angles in a better manner. Before we move forward, take a look at the five-step GMAT Preparation plan to score 700+ on the GMAT:
If you are planning to take the GMAT, we can help you with a personalized study plan and give you access to quality online content to prepare. Write to us at acethegmat@e-gmat.com. We are the most reviewed GMAT prep company on GMAT club with more than 2500+ reviews and are the only prep company that has delivered more than 700+ scores than any other GMAT club partner. Why don’t you take a free trial and judge for yourself?
Definition of Line
A line does not have any endpoints. It has an infinite length.

Definition of a Line Segment
A line segment is a segment of a line, or in other words, we can say that a line segment is a line with two endpoints.
For example, The diagram shows a line L and one segment of this line is AB.
In a plane, there can be many lines or line segments.
And, these lines can be divided into a few types based on the relative positioning of a line with another line.
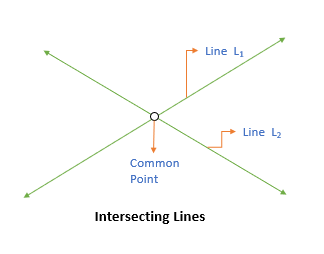
Types of lines
Intersecting Lines
Two lines are intersecting lines if they meet each other at a common point.
For example, L1 and L2 are intersecting lines in the below diagram

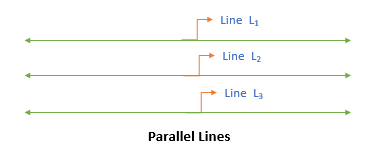
Parallel Lines
A pair of lines are parallel if they never intersect.
For example, L1, L2, and L3 are parallel lines in the below diagram.
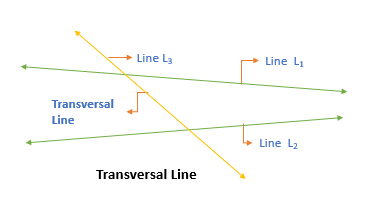
Transversal Line
A transversal line cuts two or more lines at distinct points.
For example, Line L3 is the transversal line in the below diagram.
Next, we take a look at angles and their properties.
Scoring a Q50-51 on the GMAT helps you get a 700+ GMAT score. Start your journey of getting a Q50-51 on the GMAT with e-GMAT’s AI-driven online preparation course. Our xPERT not only curates the most optimized learning path but also tracks your improvement, ensuring that you get to your target Quant score quickly and reliably. Watch this video to know more:
Are you struggling with GMAT quant? e-GMAT provides structured learning from foundations to help you master the skills needed for a high score. Join the world’s most successful prep company for a free trial and see the difference it can make. We are the most reviewed online GMAT Prep company with 2500+ reviews on GMATClub, as of March 2023.
Angle – What is it?
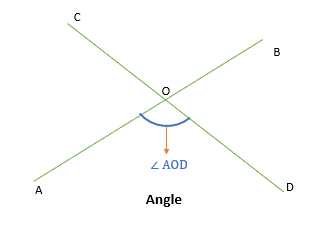
An angle is formed when two lines intersect each other. We represent an angle by the symbol ∠.
An angle involves two legs and one common vertex at which two lines meet.
For example, ∠AOD is formed when lines AB and CD intersect with each other.
Also, ∠AOD is formed between the leg AO and OD, so we include A, O, and D while naming the angle.
Do you know that the position of leg points does not matter as long as the common vertex is the middle letter in the angle name
Measurement of an Angle
The angle is measured in degrees.
An angle can measure from zero (0) degrees to 360 degrees. Based on the measurement of an angle, they are divided into four types:
- Acute angle
- Right angle
- Obtuse angle
- Reflex angle
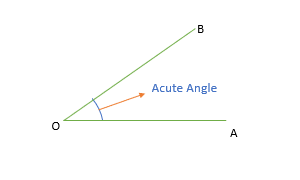
Acute Angle
When the measurement of the angle is between 0 degrees and 90 degrees.
Right Angle
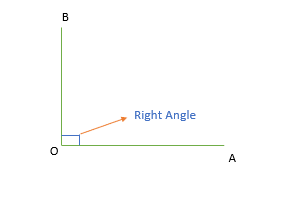
When the measurement of the angle is exactly 90 degree.
- If there is a right angle between two lines, then the two lines are said to be perpendicular to each other.
Obtuse Angle
When the measurement of the angle is between 90 degrees and 180 degrees.
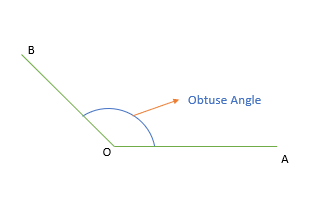
A straight line has an angle of 180 degrees.
Reflex Angle
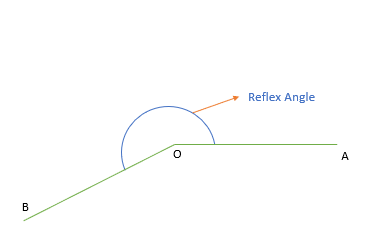
When the measurement of the angle is between 180 degrees and 360 degrees.
We have discussed the basic type of angles.
Let us now discuss the angles formed when two lines intersect each other.
If you are planning to take the GMAT, we can give you access to quality online content to prepare. We are the most reviewed GMAT prep company on gmatclub with more than 2500+ reviews, as of March 2023.
Angles formed between two intersecting lines
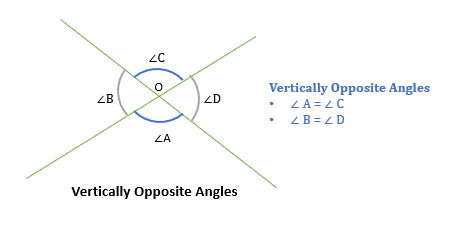
Vertically Opposite Angles
When two lines intersect each other, then 4 angles are formed.
- And, the angles that are opposite to each other at the intersection point are known as vertically opposite angles.
- Vertically opposite angles are always equal.
Let us now discuss the angles formed when two lines are intersected by a third line i.e. a transversal line.
Angles formed by a transversal line

When a transversal line intersects two lines, then eight angles are formed as shown.
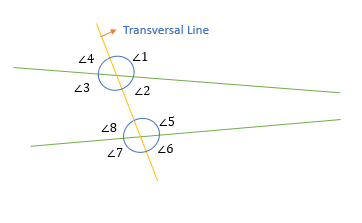
Now, there are several special pairs of angles that are obtained from this diagram.
For example: If you notice (∠1, ∠3), (∠2, ∠4), (∠5, ∠7), and (∠6, ∠8) are all vertically opposite angles.
Similarly, we get several other types of angles. Let us discuss them.
Other types of Angles
Interior and Exterior Angles
Interior angles are the ones that are present inside the region between two lines.
- And, exterior angles are the ones that are not present inside this region.
For example:
- ∠2, ∠3, ∠5, and ∠8 are interior angles.
- And, ∠1, ∠4, ∠6, and ∠7 are exterior angles.
Corresponding Angles
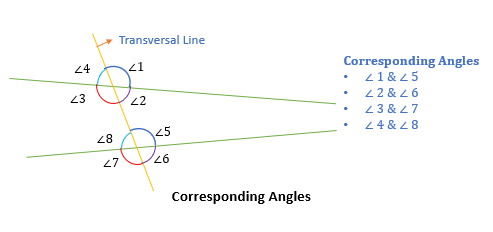
Two angles are said to be corresponding angles if they lie on the same side of the transversal line such that:
- One angle is an interior angle, and
- Another is an exterior angle
For example:
(∠4, ∠8), (∠3, ∠7), (∠1, ∠5), and (∠2, ∠6) are 4 pairs of corresponding angles
Alternate interior angles
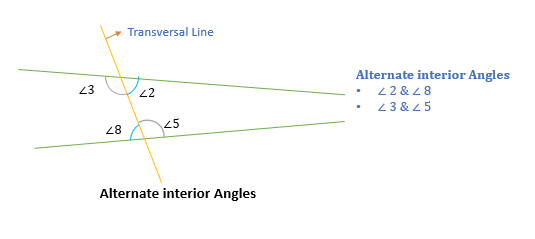
Two interior angles, present on the opposite side of a transversal line, are called alternate interior angles.
For example:
- (∠2, ∠8) and (∠3, ∠5) are alternate interior angles.
Alternate exterior angles
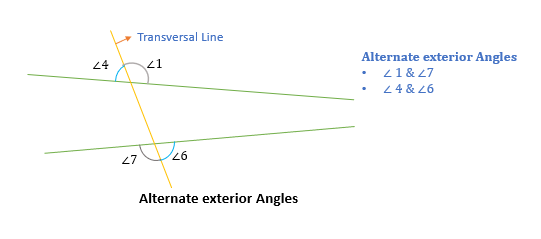
Two exterior angles that are present on the opposite side of the transversal line are called alternate exterior angles.
For example:
- (∠1, ∠7) and (∠4, ∠6) are alternate exterior angles.
Note: If a transversal line intersects two parallel lines, then the corresponding angles, alternate interior angles, and alternate exterior angles are equal.
So, we have discussed all the type of angles.
Let us now learn about a few properties of angles.
Properties of Angles
Sum of angles on one side of a straight line
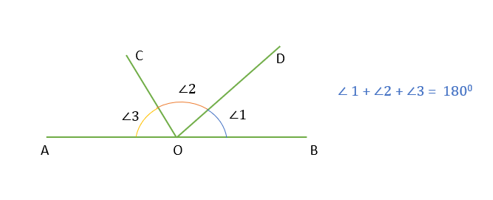
The sum of all the angles on one side of a straight line is always 180 degrees.
For example, The sum of ∠1, ∠2, and ∠3 is 180 degrees.
Sum of angles around a point
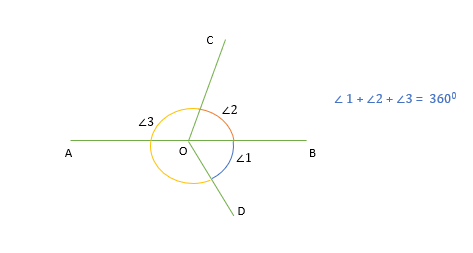
Take a free GMAT mock to understand your baseline score and start your GMAT prep with our free trial. We are the most reviewed online GMAT Prep company with 2500+ reviews on GMATClub
The sum of all the angles around a point is always 360 degrees.
For example, Sum of angles (∠1, ∠2, and ∠3) around point O is 360 degrees.
If you liked this article, here are a few more articles that you may like:
- Properties of Quadrilateral
- Properties of a Circle
- Properties of Triangles
- GMAT Geometry Formulas and Concepts on Triangles
Application of Lines and Angles Properties in Questions
Lines and Angles – Question 1
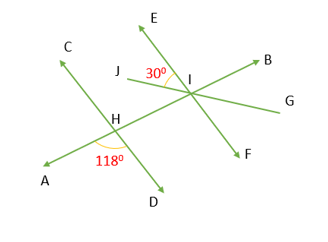
In the diagram given above, the line CD is parallel to line EF. If ∠AHD and ∠JIE are 118° and 30° respectively, then what is the measure of angle GIB?
- 30
- 32
- 34
- 40
- 62
Solution
Step 1: Given
- line CD is parallel to line EF.
- ∠AHD =118°
- ∠JIE = 30°
Step 2: To find
- Measure of angle ∠GIB
Step 3: Approach and Working out
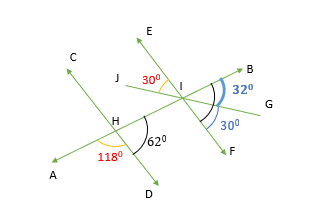
We need to find the measure of angle GIB.
- So, with the given information, we know that line CD is parallel to line EF and line AB is transversal to them.
- Hence, ∠DHI = ∠FIB as both are corresponding angles.
- We can find ∠DHI or ∠FIB as
- ∠AHD + ∠DHI = 180°
- 118°+ ∠FIB = 180°
- ∠FIB = 62°
- Now, ∠FIB = ∠FIG + ∠GIB
- By observing the diagram, ∠FIG = ∠JIE as these are vertically opposite angles between EF and JG.
- ∠FIB = ∠FIG + ∠GIB
- 62° = ∠JIE + ∠GIB
- 62° = 30° + ∠GIB
- ∠GIB = 32°
- We can find ∠DHI or ∠FIB as
- Hence, ∠DHI = ∠FIB as both are corresponding angles.
Hence, the correct answer is option B.
Lines and Angles – Question 2
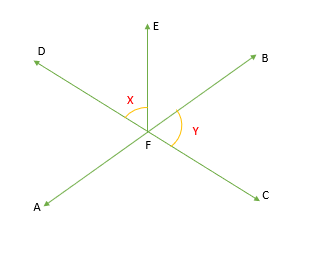
In the diagram given above, angle DFE and angle BFC are represented by X and Y respectively. If ∠AFC = 100° and ∠BFE = 45°then what is the value of Y-X?
- 20
- 25
- 30
- 35
- 40
Solution
Step 1: Given
- ∠DFE = X
- ∠BFC = Y
- ∠AFC = 100°
- ∠BFE = 45°
Step 2: To find
- The value of Y-X
Step 3: Approach and Working out
To find Y-X, we need to find Y and X first.
Measure of angle Y:
- We are given ∠AFC = 100° and,
- ∠AFC + ∠BFC = 180° as the sum of angles on the same side straight line is 180°
- 100° + ∠BFC = 180°
- ∠BFC = Y = 80°
Measure of angle X:
- We are given ∠BFE = 45° and,
- ∠DFE + ∠BFE + ∠BFC = 180° as the sum of angles on the same side straight line is 180°.
- X + 45° +80°= 180°
- X = 55°
Hence, Y – X = 80° – 55° =25°.
Thus, the correct answer is option B.
If you are planning to take the GMAT, we can give you access to quality online content to prepare. We are the most reviewed GMAT prep company on gmatclub with more than 2500+ reviews, as of March 2023.