In this article, we are going to learn about the simplest form of a polygon, a triangle. All polygons can be divided into triangles, or in other words, they are formed by combining two or more triangles. Thus, understanding the basic properties of a triangle and its types is essential.
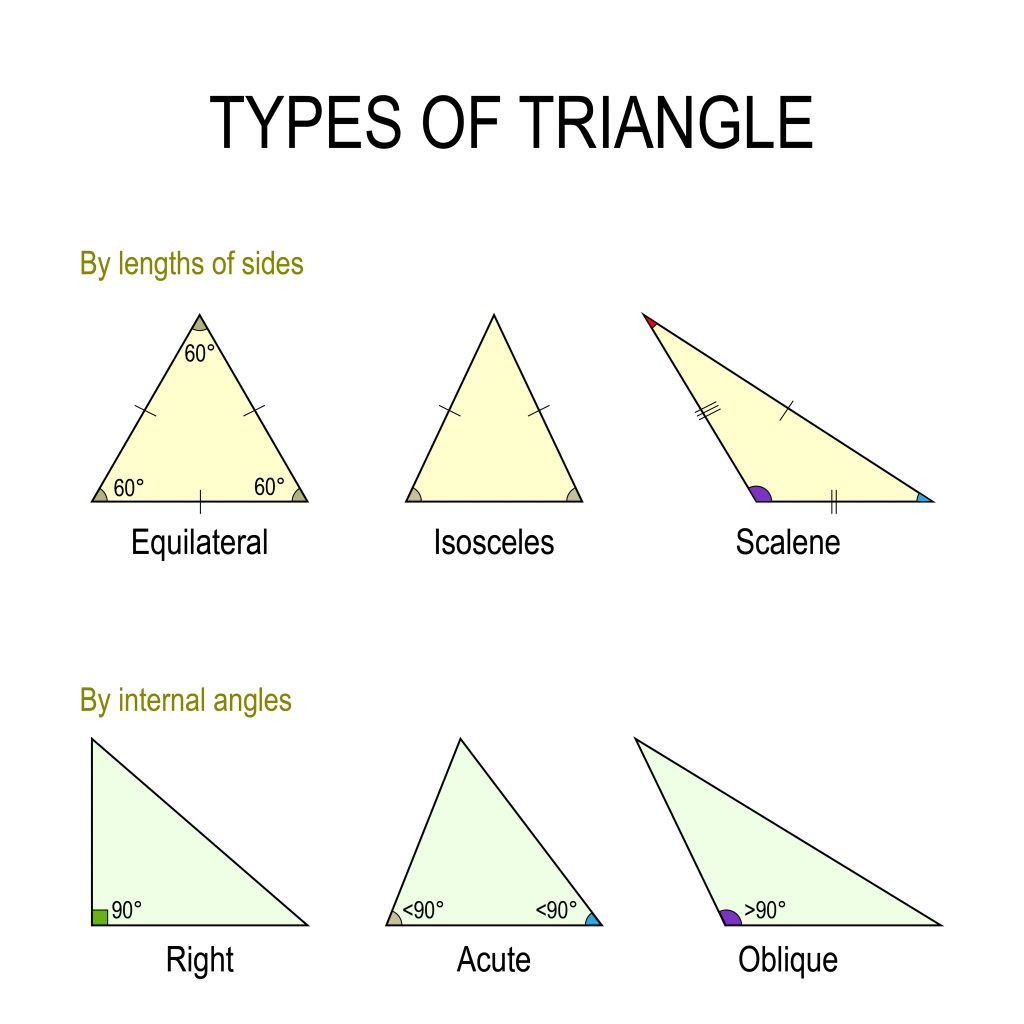
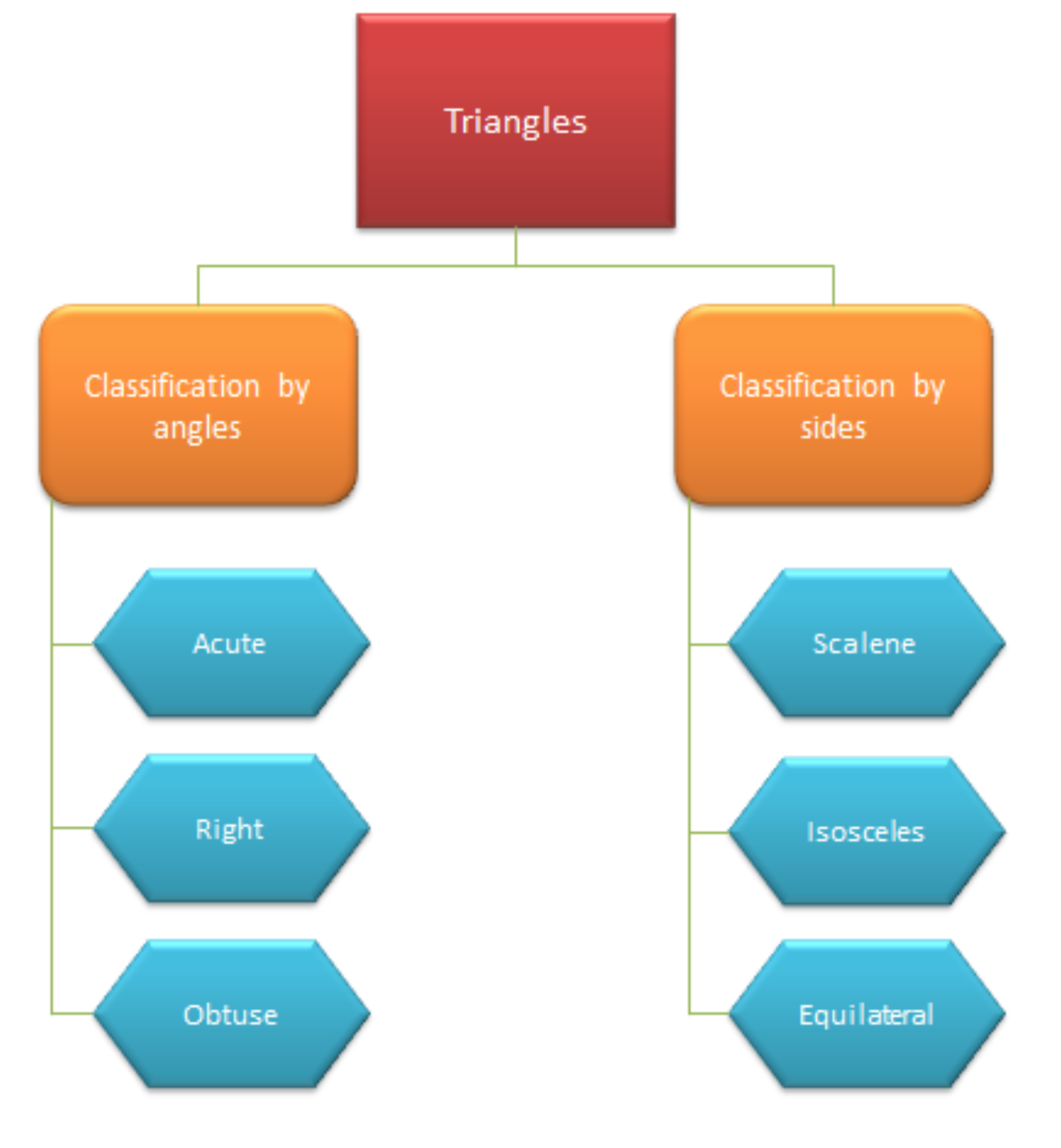
There are six types of triangles in total – Isosceles, Scalene, Equilaterial, Oblique, Acute, and Right. Based on the classification according to internal angles, there are three types – Equilateral, Isosceles, and Scalene. Whereas, the types of a triangle that are classified according to the length of its side are Right, Acute, and Oblique. Here are the types of triangles:
| Based on the Angle | Based on the Sides |
| Acute Angled Triangle | Equilateral Triangle |
| Oblique angled Triangle | Scalene Triangle |
| Right Angle Triangle | Isosceles Triangle |
Watch this video to know the basic properties of triangle:
Questions on triangles are very commonly asked on the GMAT. Ace GMAT Quant by signing up for our free trial and get access to 400+ questions. We are the most reviewed online GMAT Prep company with 2500+ reviews on GMATClub.
What is a triangle?
As the name suggests, the triangle is a polygon that has three angles. So, when does a closed figure has three angles?
When it has three line segments joined end to end.
Thus, we can say that a triangle is a polygon, which has three sides, three angles, three vertices and the sum of all three angles of any triangle equals 180°.
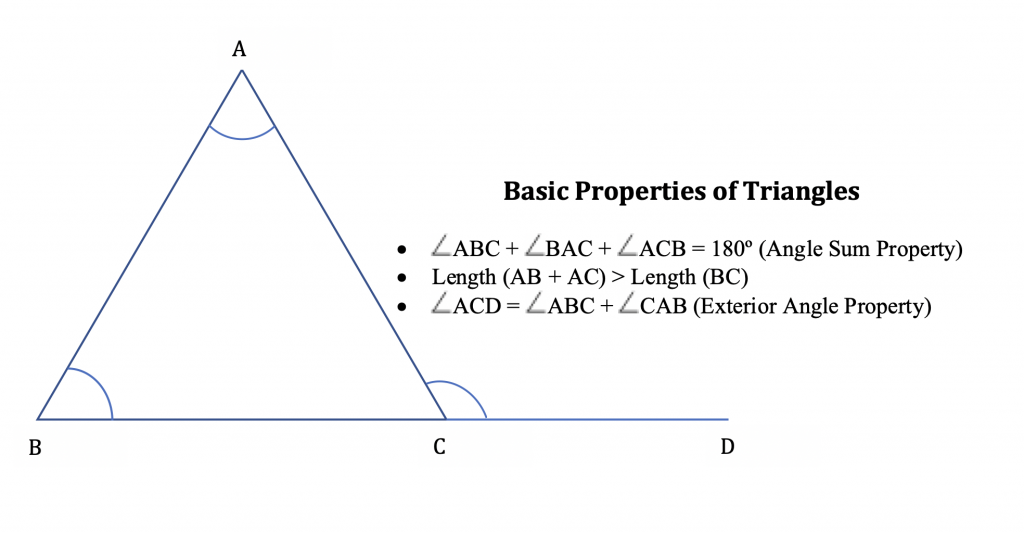
Properties of a triangle
The properties of a triangle are:
- A triangle has three sides, three angles, and three vertices.
- The sum of all internal angles of a triangle is always equal to 180°. This is called the angle sum property of a triangle.
- The sum of the length of any two sides of a triangle is greater than the length of the third side.
- The side opposite to the largest angle of a triangle is the largest side.
- Any exterior angle of the triangle is equal to the sum of its interior opposite angles. This is called the exterior angle property of a triangle.
Did you know that a high GMAT score can increase your chances of admission to your dream B-school? Moreover, a GMAT score of 730+ yields an incremental $500k in ROI. Here is how we can help:
Begin your GMAT preparation with the only prep company that has delivered more 700+ scores than any other GMAT club partner. Achieve GMAT 740+ with our AI driven tools that you personalized feedback at every step of your GMAT journey. Take our free trial today!
Types of triangles
Triangles can be classified in 2 major ways:
- Classification according to internal angles (Right, Acute, Oblique)
- Classification according to the length of its sides (Equilateral, Isosceles, Scalene)
Let’s look into the six types of triangles in detail:
- Acute Angled Triangle
- Right-Angled Triangle
- Oblique Angled Triangle
- Scalene Angled Triangle
- Isosceles Angled Triangle
- Equilateral Angled triangle
Acute Angle Triangle
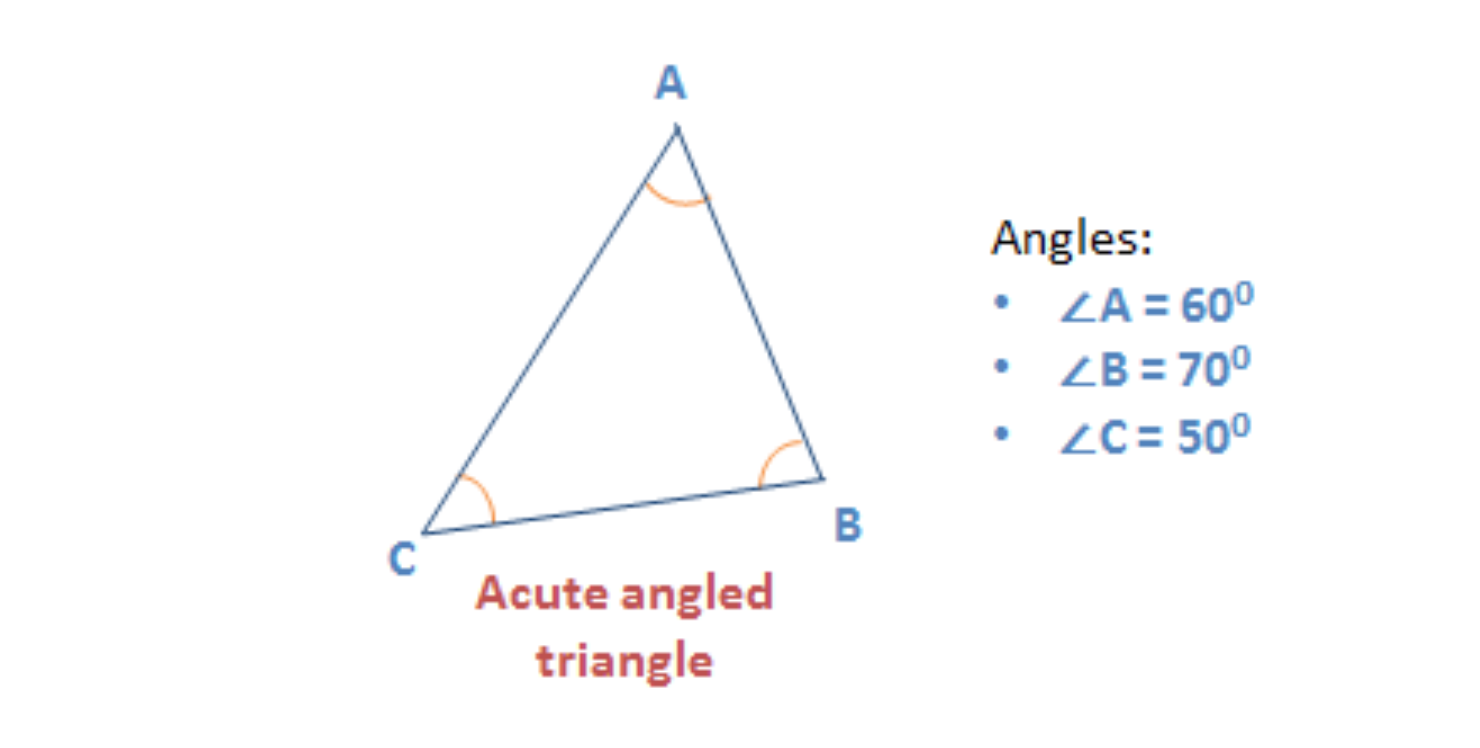
A triangle that has all three angles less than 90° is an acute angle triangle.
- So, all the angles of an acute angle triangle are called acute angles
Given below is an example of an acute angle triangle.
Right-Angle Triangle
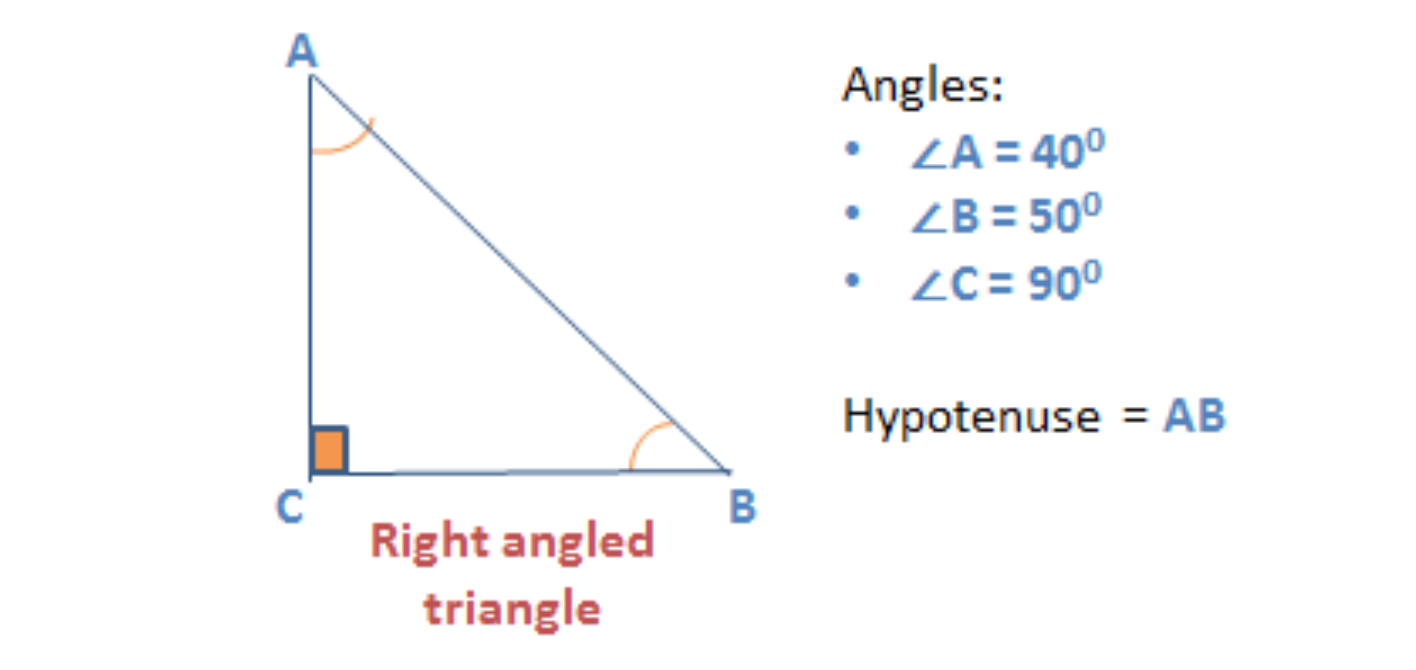
A triangle that has one angle that measures exactly 90° is a right-angle triangle.
- The other two angles of a right-angle triangle are acute angles.
- The side opposite to the right angle is the largest side of the triangle and is called the hypotenuse.
In a right-angled triangle, the sum of squares of the perpendicular sides is equal to the square of the hypotenuse.
For e.g. considering the above right-angled triangle ACB, we can say:
(AC)^2 + (CB)^2 = (AB)^2
This is known as Pythagoras theorem
Vice versa, we can say that if a triangle satisfies the Pythagoras condition, then it is a right-angled triangle.
Obtuse/Oblique Angle Triangle | Properties of Triangle
A triangle that has one angle that measures more than 90° is an obtuse angle triangle.
Given below is an example of an obtuse/oblique angle triangle.
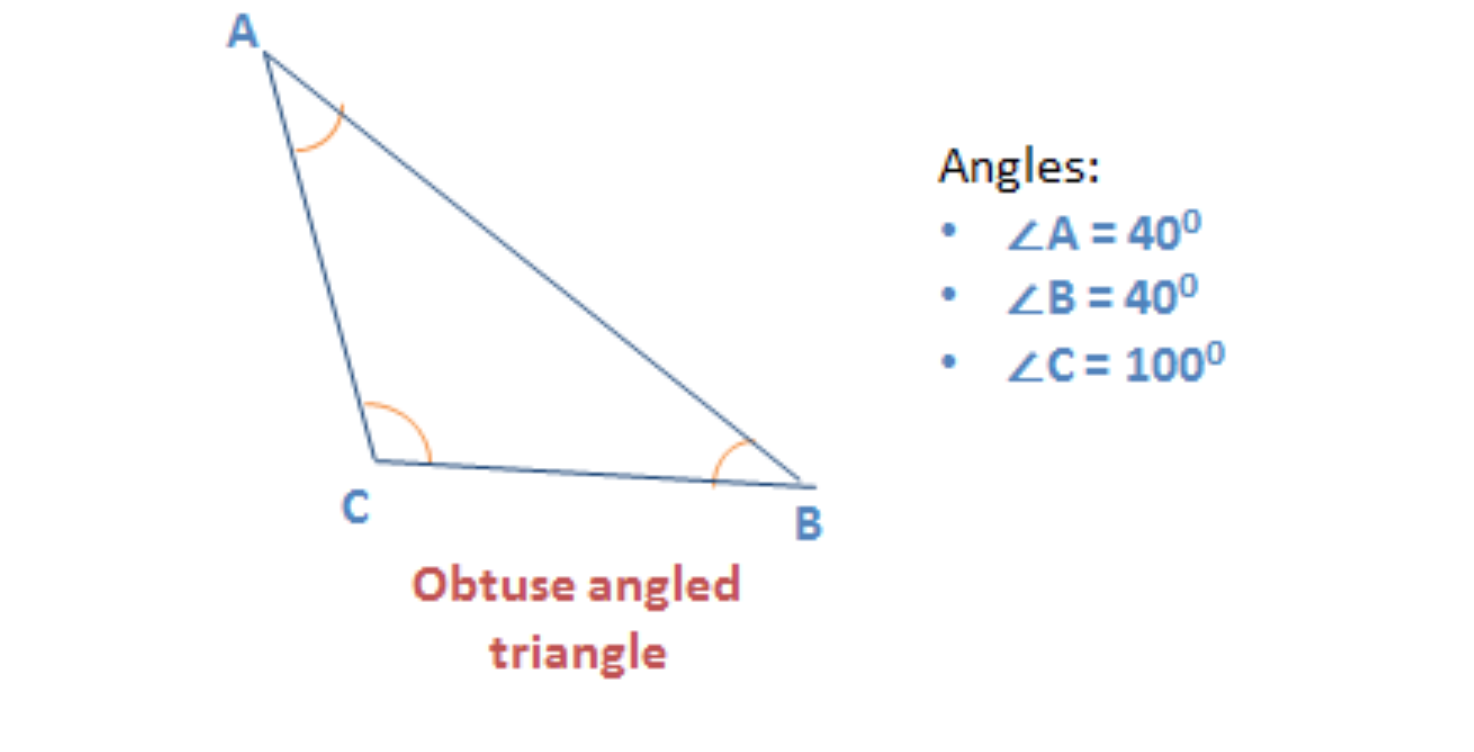
Questions on triangles are very commonly asked on the GMAT. Ace GMAT Quant by signing up for our free trial and get access to 400+ questions. We are the most reviewed online GMAT Prep company with 2500+ reviews on GMATClub.
Save 60+ hours of GMAT preparation by crafting a well-defined study plan in just 3 steps:
Scalene triangle
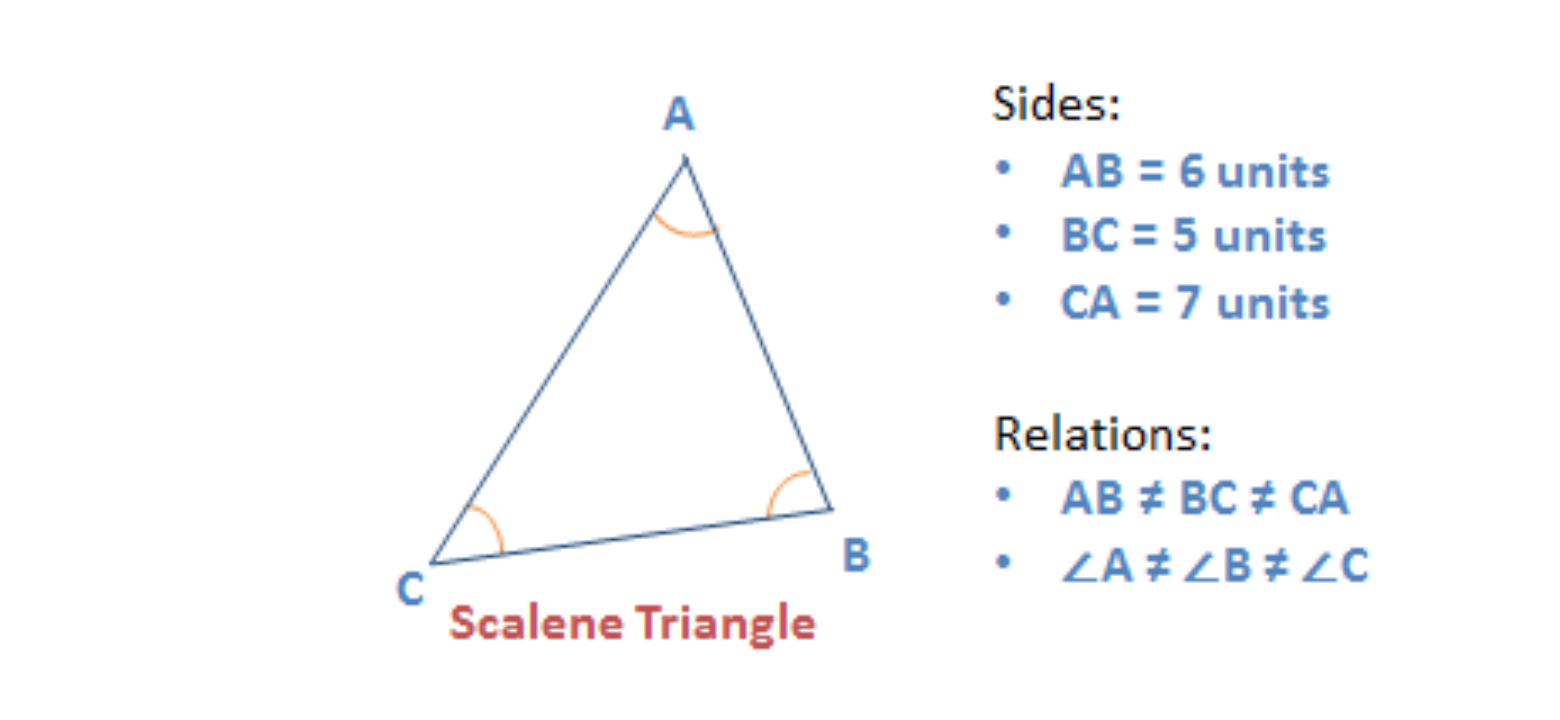
A triangle that has all three sides of different lengths is a scalene triangle.
- Since all the three sides are of different lengths, the three angles will also be different.
Given below is an example of a scalene triangle
Isosceles triangle
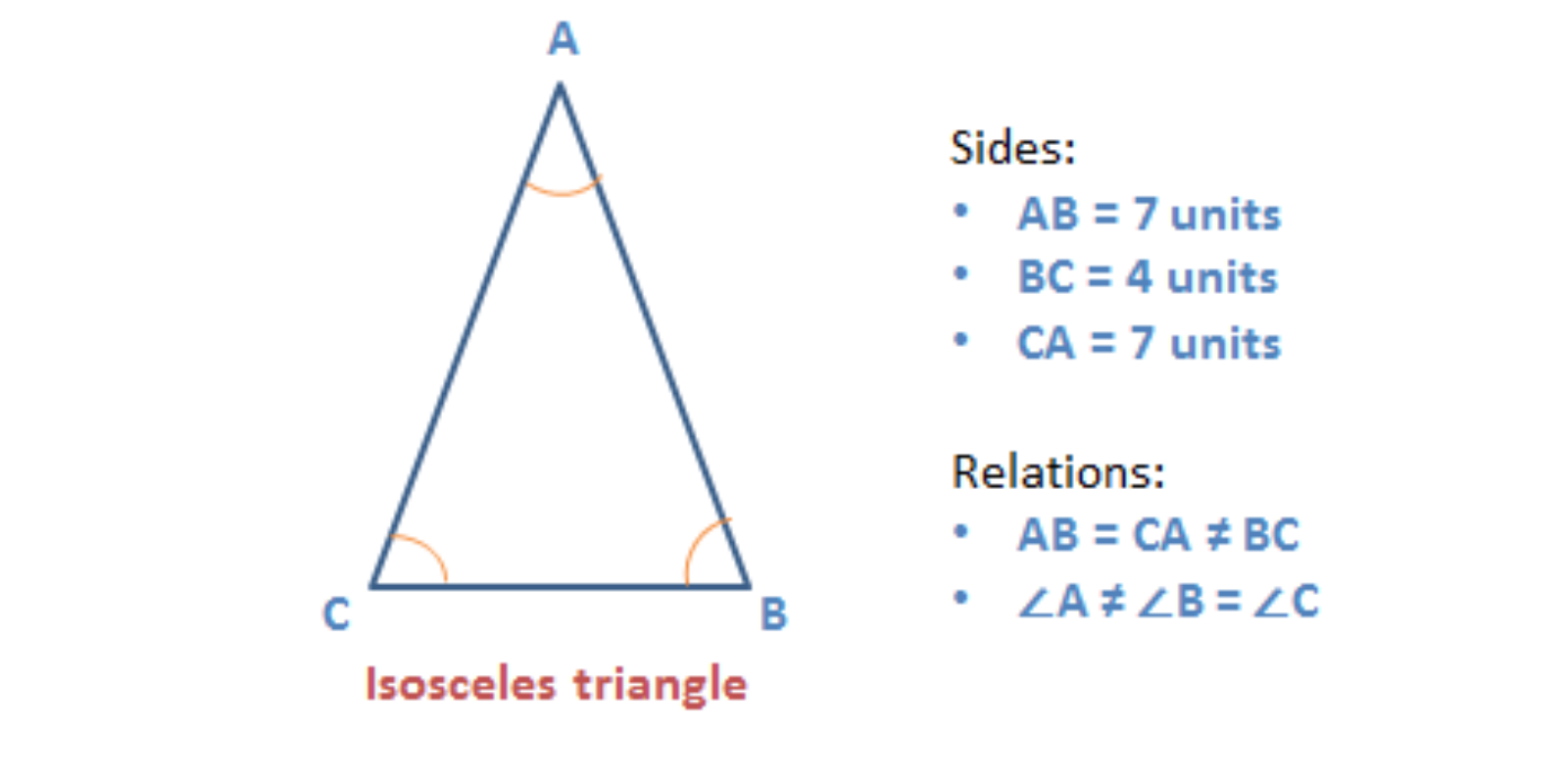
A triangle that has two sides of the same length and the third side of a different length is an isosceles triangle.
- The angles opposite the equal sides measure the same.
Given below is an example of an isosceles triangle.
Equilateral triangle | Properties of Triangle
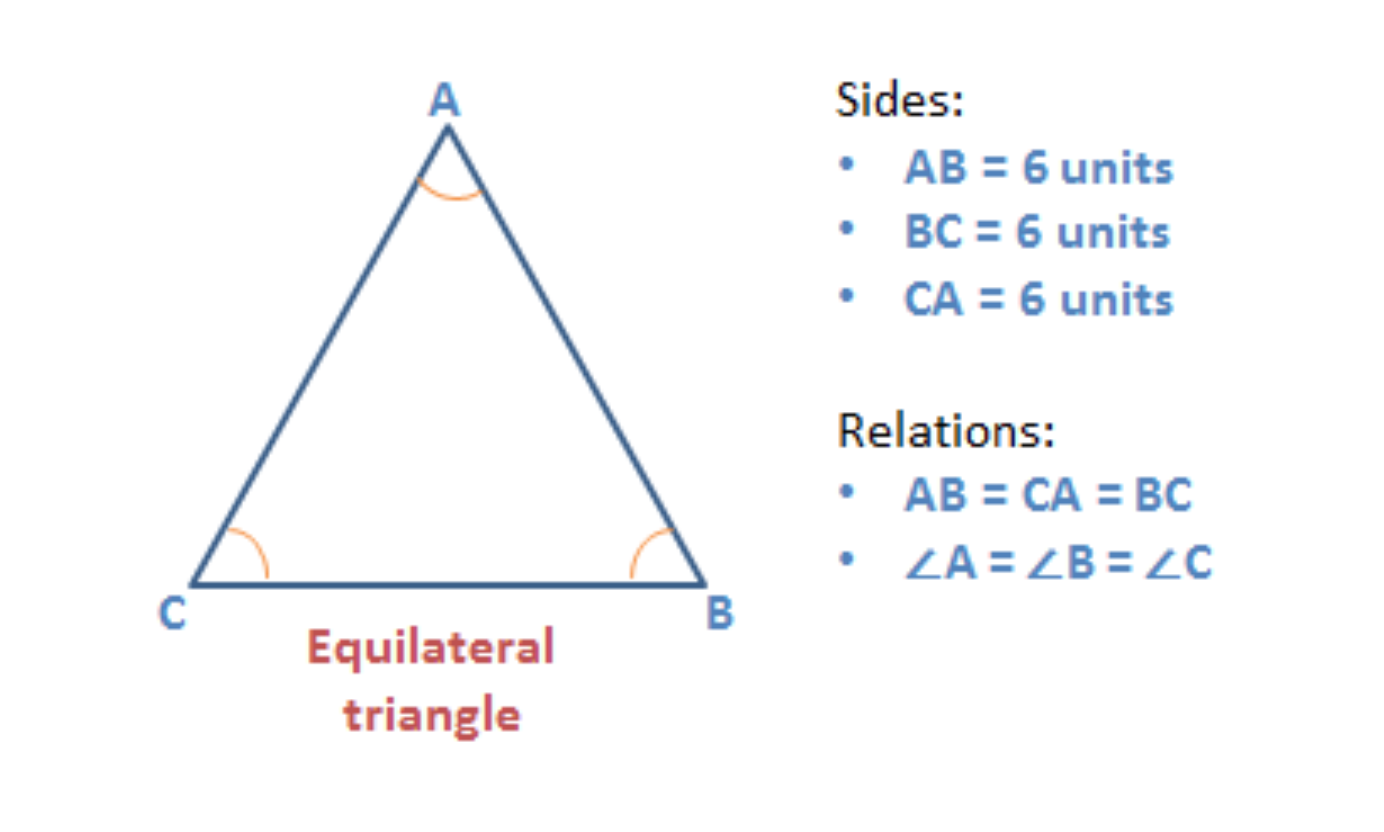
A triangle that has all three sides of the same length is an equilateral triangle.
- Since all the three sides are of the same length, all the three angles will also be equal.
- Each interior angle of an equilateral triangle = 60°
Questions on triangles are very commonly asked on the GMAT. Ace GMAT Quant by signing up for our free trial and get access to 400+ questions. We are the most reviewed online GMAT Prep company with 2500+ reviews on GMATClub.
Special cases of Right Angle Triangles | Special properties of Triangle
Let’s also see a few special cases of a right-angled triangle
45-45-90 triangle
In this triangle,
- Two angles measure 45°, and the third angle is a right angle.
- The sides of this triangle will be in the ratio – 1: 1: √2 respectively.
- This is also called an isosceles right-angled triangle since two angles are equal.
30-60-90 triangle
In this triangle,
- This is a right-angled triangle, since one angle = 90°
- The angles of this triangle are in the ratio – 1: 2: 3, and
- The sides opposite to these angles will be in the ratio – 1: √3: 2 respectively
- This is a scalene right-angled triangle since all three angles are different.
Area of Triangle
- Area of any triangle = ½ * base * height
- Area of a right-angled triangle = ½ * product of the two perpendicular sides
Properties of Triangle: Summary & Key Takeaways
Let us summarize some of the important properties of a triangle.
- The sum of all interior angles of any triangle is equal to 180°
- The sum of all exterior angles of any triangle is equal to 360°
- An exterior angle of a triangle is equal to the sum of its two interior opposite angles
- The sum of the lengths of any two sides of a triangle is always greater than the length of the third side
- Similarly, the difference between the lengths of any two sides of a triangle is always less than the length of the third side
- The side opposite to the smallest interior angle is the shortest side and vice versa.
- Similarly, the side opposite to the largest interior angle is the longest side and vice versa.
- In the case of a right-angled triangle, this side is called the hypotenuse
- The height of a triangle is equal to the length of the perpendicular dropped from a vertex to its opposite side, and this side is considered the base
If you liked this article, you may also like to read the following advanced level articles on triangles
- GMAT Geometry Concepts and Formulas on Triangles (Part-1)
- Properties of Triangles: Practice Questions (Part-2)
- Special Properties of Triangles (Part-3)
Starting with your GMAT preparation? Here is a 5 step preparation plan to ace the GMAT:
Take a free GMAT mock to understand your baseline score and start your GMAT prep with our free trial. We are the most reviewed online GMAT Prep company with 2500+ reviews on GMATClub
Properties of Triangle: Practice Question
Question: 1
In an isosceles triangle DEF, if an interior angle ∠D = 100° then what is the value of ∠F?
- 20°
- 40°
- 60°
- 80°
- 100°
Solution
Step 1: Given
- ∆DEF is an isosceles triangle
- ∠D = 100°
Step 2: To find
- The value of ∠F
Step 3: Approach and Working out
- We know that the sum of all interior angles in a triangle = 180°
- Implies, ∠D + ∠E + ∠F = 180°
- ∠E + ∠F = 1800 – 1000 = 80°
- Since ∆DEF is an isosceles triangle; two of its angles must be equal.
- And the only possibility is ∠E = ∠F
- Therefore, 2∠F = 80°
- Implies, ∠F = 40°
Hence the correct answer is Option B.
Question 2
In a right-angled triangle, ∆ABC, BC = 26 units and AB = 10 units. If BC is the longest side of the triangle, then what is the area of ∆ABC?
- 120
- 130
- 240
- 260
- 312
Solution
Step 1: Given
- ∆ABC is a right-angled triangle
- BC = 26 units
- AB = 10 units
- BC is the longest side of the triangle
Step 2: To find
- The area of triangle ∆ABC
Step 3: Approach and Working out
- We are given that BC is the longest side of the triangle, which implies that BC is the hypotenuse
Thus, according to Pythagoras rule:
- BC2 = AB2 + AC2
- 262 = 102 + AC2
- AC2 = 676 – 100 = 576
- Therefore, AC = 24 units
- We know that the area of a right-angled triangle = ½ * product of the two perpendicular sides = ½ * AB * AC = ½ * 10 * 24 = 120 sq. units
Hence the correct answer is Option A.
For more practice questions on triangles and geometry, sign up for our free trial. We have more than 400+ practice questions and 10+ hours of AI-driven video lessons.
Here are a few more articles that you may like to read:
- Properties of Quadrilateral
- Properties of Numbers: Even/Odd, Prime, and HCF & LCM
- Properties of Circle
- Properties of Lines and Angles
Did you know e-GMATers have reported more 700+ scores than ever before in GMAT Club’s history? Watch this video to understand how e-GMAT has achieved this record-shattering result by investing and innovating with a single goal in mind – To create a platform that empowers students to achieve and deliver their very best.
If you are planning to take the GMAT, we can help you with a personalized study plan and give you access to quality online content to prepare. Write to us at acethegmat@e-gmat.com. We are the most reviewed GMAT prep company on gmatclub with more than 2400 reviews and are the only prep company that has delivered more than 700+ scores than any other GMAT club partner. Why don’t you take a free trial and judge for yourself?
FAQ – Properties of a triangle
A triangle is a closed figure with three sides, three vertices, three angles, and the sum of internal angles is 180°
Triangles can be classified in 2 ways, according to internal angles and according to the length of the sides. According to internal angles, there are three types of triangles i.e., acute, right, and obtuse-angled triangle. According to the length of sides, triangles can be classified into 3 categories i.e., Scalene, Isosceles, and Equilateral triangle.
A triangle that has all three sides of different lengths is a scalene triangle.
A triangle that has two sides of the same length and the third side of a different length is an isosceles triangle.
A triangle that has all three sides of the same length is an equilateral triangle.


![Properties of Triangle – types & formulas [Video & Practice]](https://e-gmat.com/blogs/wp-content/uploads/2019/07/Properties-of-triangles-Classification-of-Triangles.jpg)










