A 10 min read

A polygon is a two-dimensional closed figure made up of at least 3 line segments. Polygons, as a topic, will pose some of the most challenging GMAT Math questions. Most of those GMAT Math questions test your understanding on Polygons through Rectangles and Squares. However, those questions are not tough intrinsically but are made tricky to exploit the gaps in your understanding. So that you don’t struggle with these questions we have identified 3 common mistakes that most GMAT test takers make. Avoid these 3 mistakes and improve your accuracy in GMAT math questions on Polygons. In this article, we will point out those 3 mistakes with the help of illustrative questions. The highlights of this article are as follows

• Why should you read this article on Polygons?
• How will you improve accuracy in GMAT Math questions on Polygons?
• Common Mistake 1 to avoid while attempting questions on Polygons
• Common Mistake 2 to improve understanding of GMAT Polygons
• Common Mistake 3 to improve accuracy in GMAT Math questions
• Takeaways to avoid mistakes in GMAT Math questions on Polygons

Why should you read this article on Polygons?

• Are you someone who gets confused while solving questions related to polygons or regular polygons?
• Does making incorrect assumptions while solving polygon questions lead you to the incorrect answer?

If the answer is yes, to any one of the above statements, then this article will help you gain better clarity and avoid mistakes in the GMAT.

For any strategic advice for GMAT or MBA Admissions, write to us at acethegmat@e-gmat.com. Take a free trial and get unlimited access to concept files, live sessions, and practice questions.

How will you improve accuracy in GMAT Math questions on Polygons?

To help you improve accuracy in GMAT polygons, we will discuss the following –

• Dive into the details of applying formulae to find the relation between the interior and the exterior angles of a regular polygon.
• Discuss the important geometric properties of regular polygons.
• Help you solidify your conceptual understanding through examples and
• Highlight the common mistakes made by students so that those can be avoided while solving the questions.

We will discuss all these with the help of 3 GMAT Math Questions. We’ll use data sufficiency questions in this article.

We have also illustrated common mistakes in GMAT Geometry questions on Triangles through Problem Solving questions

Let us start our discussion by looking at our first question.

Mistake 1: Incorrect Assumption of Regular Polygon

Question 1.

Find the measure of the internal angle of a six-sided polygon.

Statement 1: One of the exterior angles of the polygon is 60°.

Statement 2: The sum of the interior angles is 720°.

• (A)  Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
• (B)  Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
• (C)  BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
• (D)  EACH statement ALONE is sufficient to answer the question asked.
• (E)  Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

Solution:

In every Data Sufficiency question, before analyzing the statements, we should first analyze the question stem and try to figure out any relevant information, that we can use to solve the question.

• The question only mentions that we have a six-sided polygon.

What we need to find out is the measure of an internal angle of the six-sided polygon.

As we don’t have any other relevant information available, let’s proceed with the analysis of the statements.

Improving accuracy for the GMAT is important but GMAT is more of a test of ability. Learn how can you leverage the adaptive nature of the GMAT to score high.

Common Error 1:

As per the given information in statement 1, one of the exterior angles of the polygon is 60°.

• Do you think that this statement is sufficient to answer the question? Let’s see.

We know, for an n-sided polygon,

The answer is no!

We got the measure of one of the six internal angles of the polygon. But what about the other 5 internal angles? Will they be the same?

• Not necessarily.
• They will be the same only when the polygon is a regular polygon. This is an assumption that we made while concluding that statement 1 is sufficient.

Many students fall into this trap of assuming the polygon in the question to be a regular polygon and hence select the wrong answer.

It is not mentioned in the question that this is a regular polygon and hence we cannot make the conclusion.

Let us now look at the solution to this question by analyzing the given statements:

Analyzing Statement 1:

Now, in the first statement we are given information about one of the exterior angle of the six-sided polygon:

• We know that one exterior angle is 60°
  • Therefore, the corresponding interior angle is 120°.
• But, it is nowhere given in the question, that the polygon in the question is a regular polygon.
  • Therefore, we cannot make any conclusion about the other interior angles.

Hence statement 1 is insufficient.

Do you know, you can save up to $624 or INR 43,000 on your GMAT costs. Learn how in this article.

Common Error 2:

As per statement 2, we are given the sum of the interior angles as 720°.

• As it is a 6-sided polygon, the measure of an internal angle must be equal to =  (720°/6) = 120°.

Hence, we have sufficient information in statement 2 to answer the question.

Wait! Aren’t we assuming again that all the internal angles are equal?

• But that is true only when we have a regular polygon.
• As in this question, there is no mention whether the polygon is regular or not, we can’t conclude that statement 2 is sufficient to answer the question.

Correct Approach & Solution

Now that the statements are individually not sufficient, let’s combine them to see whether we can determine the answer or not.

From statement 1 & 2 we can infer that

• One of the interior angles is 120° and
• The sum of the interior angles is 720°
  • But, since we still cannot infer that if it is a regular polygon or not, both the statements combined are insufficient to find the answer.

Hence the correct answer choice is option E.

Key Takeaways for Question 1:

From this question we have the following key takeaways:

• We have seen that we must not assume a polygon to be a regular polygon unless some specific information is provided in the question or in the supporting statements.

To ace the GMAT, avoiding common mistakes is important, so is devsing an effective study plan. Learn how to manage your job and GMAT preparation with a rock solid study plan

The devil is in the details! Planning out the finer details of your study schedule takes you one step closer to your target GMAT score. Learn the other benefits of a well defined study plan in this article.

Save 60+ hours of GMAT preparation by crafting a well-defined study plan in just 3 steps:

Mistake 2: Lack of conceptual clarity related to regular polygons

Now let us take another example, to solidify our understanding of regular polygons:

Question 2.

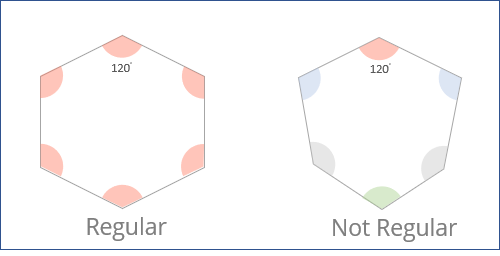
Is the 6-sided polygon regular?

Statement 1: All the sides are equal

Statement 2: All the internal angles of the polygon are equal

Solution:

Before we move forward with discussing this question, can you identify how many of the following two statements are true?

• If all the sides of a polygon are equal, it is a regular polygon.
• If all the internal angles of a polygon are equal, it is a regular polygon.

If we are considering a regular polygon, then both the statements must be simultaneously true.

Now let us analyze the question to understand this in more detail.

• The question mentions that we have a 6-sided polygon.
• We need to find out whether the polygon is a regular polygon or not.

As we don’t have any other statement in the question stem, let’s move forward to analyze the statements.

We are sure, reading this article would increase your ability. But how will you measure your current ability? Learn in this article.

Common Error 1:

• As per the given information in statement 1, all the sides of this 6-sided polygon are equal.
• First, let us take an example of a 4-sided polygon for better understanding.

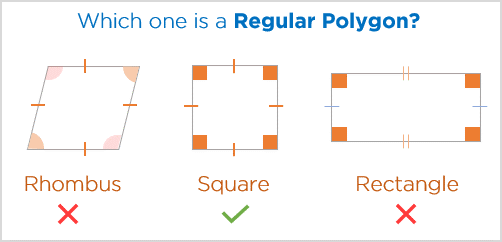
The above figure is a Rhombus. Now we know that a rhombus has the following properties:

• All sides are equal
• Opposite angles are equal

Now, let’s analyze the second statement.

Common Error 2:

• Statement 2 says all the angles of the given polygon are equal.
  • Let us take an example of another 4-sided polygon for better understanding.
• We know that a rectangle has the following properties:
  • All internal angles are equal
  • Opposite sides are equal in length

• It means the rectangle must be a regular polygon, right?

• The answer is NO

Correct Approach & Solution

Now that we can’t find the individual statements sufficient let us combine them.

From statements 1 and 2, we know:

• All sides of the polygon are equal.
• And all internal angles of the polygon are also equal.

Now, recall what we mentioned at the beginning of this question about regular polygon?

• A regular polygon must have all the sides equal to each other, as well as all the angles same.
  • This is exactly what we concluded by combining the two statements.
• Hence, we can sufficiently say that the polygon is a regular polygon.

Thus, the correct answer is Option C

Key Takeaways for Question 2:

From the above question we can make a note of the following key takeaways:

• We must possess 200% clarity of concepts related to both polygons and regular polygons.
• And we must be aware of the key differences between them while solving GMAT Math questions.

A 200% clarity of concepts will help you ace the GMAT. Clarity about your MBA application will help you get into your dream Business School. Learn how to get into a top Business School

Read our articles on how to get into Harvard and Stanford.

Mistake 3: Lack of conceptual clarity related to diagonals of 4 sided figures

Now, let us take the final type of commonly made error committed by the students in questions related to Polygons and rectangles.

The following question will help in illustrating this:

Question 3

What is the perimeter (P) of a rectangle Q?

Statement 1: The diagonal of the rectangle is 13 units.

Statement 2: The area of the rectangle is 60 sq. units.

Solution:

The question asks us to find out the perimeter (P) of a rectangle, Q.

We know, to determine the perimeter of a rectangle, we need to have the measures of length and width of the rectangle.

As we don’t have any other information to consider, let’s analyze the given statements.

Common Error 1:

• As per the information given in statement 1, the diagonal of the rectangle is 13 units.

Let us draw a figure to represent the information given in the statement above:

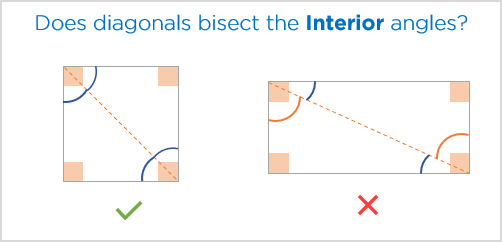
• We are given the length of the diagonal of rectangle Q as 13 units
• We know that all the angles in a rectangle are right angles
  • Does the diagonal bisect the angles ABC and ADC?
  • Yes, the diagonals do bisect the attached angles with them.
• Thus, we can say that angle DBC = angle BDC = 45°

• Now, if  BDC = DBC = 45°, then we can say in triangle BDC, the sides BC and CD must be equal.
• So, if we apply Pythagoras Theorem to the right-angled triangle BDC, we can write
  • BD² = BC² + CD²

Or, BD² = 2 * BC²

Or, BC = √(BD/2) = √(13/2)

Now, we know ABCD is a rectangle.

• Hence, the opposite sides are equal in length.
  • So, the perimeter of the rectangle is 2 (BC + CD)
  • As BC = CD and we know BC = √(13/2), we can replace the value and determine the perimeter of the rectangle.
• Thus, is statement 1 sufficient?

The answer to all the above questions is NO.

In the solution, we have assumed that the diagonal BD is bisecting the angles ABC and ADC.

• Following this assumption, we concluded that angle DBC and angle BDC are equal to 45°, and hence, BC = CD.
• However, this is not necessarily true for any rectangle.
• Only when the rectangle is a square, we can say the diagonals bisect the angles attached. Other than the case of a square, we cannot assume this to be true.

Thus, statement 1 is not sufficient.

What to do 3 weeks, 2 weeks, or 1 week before your scheduled GMAT date. Learn in this article.

Common Error 2:

• The area of the rectangle is given as 60 sq. units.
  • Hence, we can say the length and width of the rectangle must be 12 and 5 units respectively, as this value set satisfying the Pythagorean Theorem also: 12² + 5² = 13².
• As we already know length and width, the perimeter must be equal to 2 (12 + 5) units.

Does this make statement 2 sufficient?

If you answered yes to the above question, you need to revisit the concepts of quadrilaterals thoroughly.

When we assume the length and width as 12 and 5 respectively, we are only assuming one possible value set of length and width.

• Nowhere in the question, it was mentioned that the length and width of the rectangle is an integer.
  • Hence, they can have non-integer values also.
  • For example, 11 and 4√3 [(11)² + (4√3)² = 13²] or 10 and √69 [(10)² + (√69)² = 13²]
• As we can see we can have multiple possibilities, we can say that statement 2 is not sufficient to answer.

Correct Approach & Solution

As we didn’t find sufficient information individually from statement 1 and statement 2, we will combine them.

• From statement 1 and 2 we know that if length and width of the rectangle is l and b respectively, then
  • l² + b² = 169 and l * b = 60
• Also, perimeter (P) of a rectangle is given by 2 * (l + b)
• Now we want to find (l + b) and we have (l² + b²) and lb
  • So, we can write (l + b)² = l² + b² + 2lb = 169 + 2 * 60 = 169 + 120 = 289
    • Or, l + b = 17
  • Thus, perimeter P = 2 (l + b) = 2 * 17

As we are getting the answer by combining both the statements, the correct answer choice is option C.

Key Takeaways for Question 3:

• In case of a rectangle, we must not assume that the diagonals bisect the vertex angles into 45° each.
  • This only happens in the case of a square.
• Also, given the length of the diagonal, we should never assume any specific value set regarding the length and width of a rectangle,
  • We can determine the exact values with the help of some additional information only. Otherwise, we may get multiple cases.

With this, we come to the end of the article.

Let us summarise the key takeaways from the article:

Takeaways to avoid mistakes in GMAT Math questions on Polygons

• While solving GMAT Math questions on polygons, we must check first if we have sufficient information to determine whether the polygon is a regular polygon or not.
  • We can use the properties of a regular polygon only when we are sure that it is a regular polygon.
• Also, we must know how to differentiate between a polygon and a regular polygon to accurately solve those tricky GMAT Math Questions.
• In a rectangle, the diagonals bisect the vertex angles only when it is a square.
• Also, for a rectangle, from the length of the diagonal, we must not assume any specific value set for length and width, unless we have some additional information to determine the unique value.

You can improve accuracy with practice. To make sure you easily solve GMAT Math questions on Polygons, we also have 4 bonus practice questions for you to attempt. We’ll post these questions very soon. So, make sure you watch this space for some mind-boggling GMAT Math Questions on Polygons.

If you are planning to take the GMAT, we can help you with a personalized study plan and give you access to quality online content to prepare. Write to us at acethegmat@e-gmat.com. We are the most reviewed GMAT prep company on gmatclub with more than 2500 reviews and are the only prep company that has delivered more than 700+ scores than any other GMAT club partner. Why don’t you take a free trial and judge for yourself?