A 8 min read

The objective of this article

• The primary objective of this article is to explain the use of Visualizing the information given in a question and representing it in the form of a Tree Diagram.
• This article is helpful for those who have a basic understanding of Percent, Sets, and Elements.
• After going through the article, one will be able to solve various questions on Sets, Probability, Percent, and many more word problems simply by representing the given information in the form of a Tree Structure.

Agenda of the Article:

• In this article, we will solve 2 examples to learn the application of solving a question using a tree structure. First, we will see how to understand the given information and then represent the given information in the form of a Tree Structure with appropriate branching.

Learn how Anastasiia scored a perfect Q51 on the GMAT and received an admit from Columbia Business School.

Question 1

720 people have attended a guest lecture, which was open for only students and faculty, conducted by an MBA graduate. The number of females, who attended the lecture is half the number of males, who attended the lecture. There were four times as many students as faculty at the lecture. If 2/3 ^rd of the faculty were males, then how many female students have attended the lecture?

1. 192
2. 240
3. 288
4. 384
5. 432

Understanding the question

In this question, we are given that,

• A guest lecture conducted by an MBA graduate was attended by a total of 720 people
• And, only students and faculty were allowed to attend this lecture
  • We also have information that the number of students, who attended the lecture is equal to 4 times the number of faculty who attended the lecture.
    • Among the total number of faculty, who attended the lecture, 2/3 ^rd were males
    • And, the total number of females, who attended the lecture were half the total number of males

This is all the information that we have, and we are asked to find out the number of female students who attended the lecture.

If you are planning to take the GMAT, we can help you with a personalized study plan and give you access to quality online content to prepare. Write to us at acethegmat@e-gmat.com. We are the most reviewed GMAT prep company on gmatclub with more than 1825 reviews (as on May 25, 2019). Why don’t you take a free trial and judge it for yourself?

Set Up the Tree Diagram

Now that we have understood all the information that is given to us, let’s try to set up a Tree Diagram with proper branching

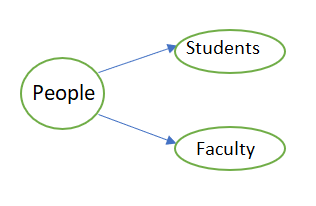
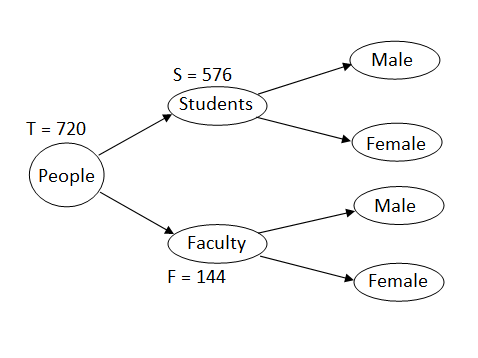
• We typically start with the main group, which in this case is the people who attended the guest lecture.
  • This group of people is sub-divided into students and faculty, since, these are only set of people who are allowed to attend the lecture.

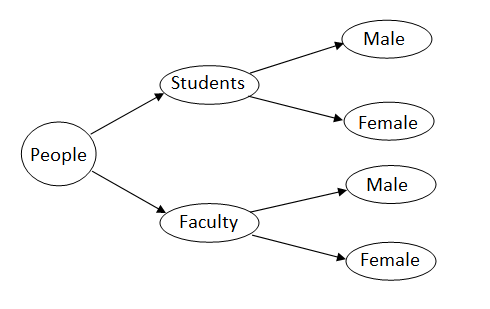
• • Now, we need to account for one more category of division, that is male and female. So, both the groups, students and faculty, are sub-divided into male and female.

Let us assume that,

• The number of Students = S
  • The number of female students = F_S, and the number of male students = M_S
• Similarly, the number of faculty = F
  • The number of female faculty = F_F and the number of male faculty = M_F

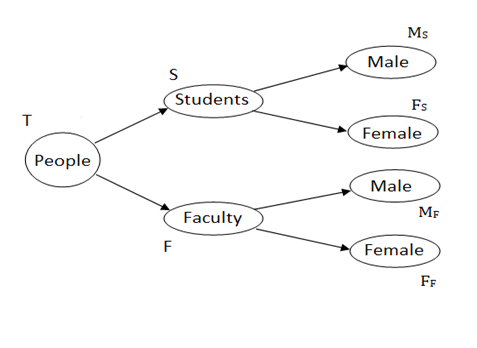
With this we have accounted space for all the branches listed in the question.

Establish Relations

The next step is to establish a relation between each and every branch with its stem.

• Let’s start with the trunk, that is, people who attended the guest lecture
• From the diagram, we can see that the total number of people(T) = the number of students(S) + the number of faculty(F), which is equal to 720
  • T = S + F = 720……… (1)
• And from the given information, we know that S = 4 * F ………. (2)
• Solving equations (1) and (2), we get
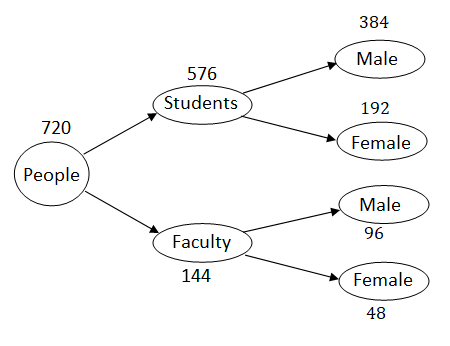
  • 4F + F =720, which implies, F = 144
  • Thus, S = 720 – 144 = 576

Now that we know the number of students and the number of faculty, let’s find how many of them are male and how many are female.

• From the Diagram, we can see that, the total number of females = F_F + F_S
  • As per the question statement, we need to find the value of F_S
  • Thus, we need to know the values of F_F and the total number of females to find F_S

To find F_F

• From the Diagram, we can see that, F = M_F + F_F
• And, from the given information, we get, M_F = (2 * F)/3 = (2 * 144)/3  = 96
  • Thus, F_F = 144 – 96 = 48

To find the total number of females

• We are told that the number of females = 1/2 * the number of males
• And from the diagram, we can infer that the total number of females + the total number of males = 720
  • Using the above two relations, we get,
    • Total number of females + 2 * total number of females = 720
    • Which implies that the total number of females = 720/3 = 240

Therefore, F_S = total number of females – F_F = 240 – 48 = 192

Now, let’s apply the learnings from this question to solve one more question, where we have more branches.

Question 2

In a law firm, 1/4 ^th of the total employees are senior employees, who have a work experience of more than 5 years and the rest are junior employees. 60 percent of the senior employees are associates and 40% of the total employees, in the firm, are junior associates. 80% of the senior employees, who are associates, are male. If the total number of male associates is equal to the total number of female associates, in the firm, then what percentage of the junior associates, in the firm, are male?

1. (31/2)%
2. (62/3)%
3. (49/2)%
4. (155/4)%
5. (245/4)%

Understanding the question

In this question, we are given that,

• In a law firm, 1/4 ^th of the employees are senior employees and the rest are junior employees.
  • We are also told that,
    • 60% of the total number of senior employees are associates, and
    • 40% of the total employees, in the firm, are junior associates
  • Then, we have another information that 80% of the senior employees, who are associates, are male

This is all the information that is given to us have, and we are asked to find out the percentage of junior associates, who are male, if the total number of male associates in the firm = the total number of female associates.

Set Up the Tree Diagram

Now that we have understood all the information that is given to us, let’s try to set up a Tree Diagram with proper branching

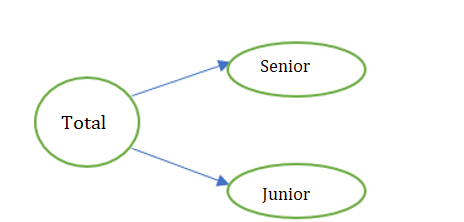
• We typically start with the main group, which is the total employees in the law firm.
  • These are sub-divided into senior employees and junior employees.

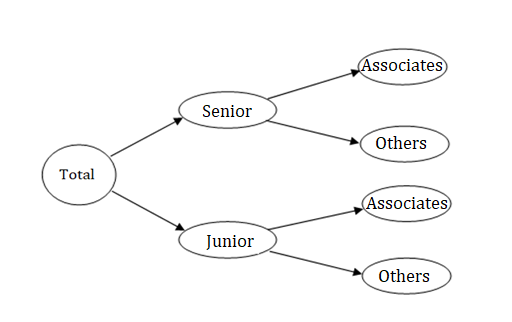
• Now, we have information about the percentage of senior and junior employees, who are associates, and the rest of the senior and junior employees can be grouped as others.

Let us assume that,

• The number of employees in the firm = N
  • The number of senior employees = S, and the number of junior employees = J

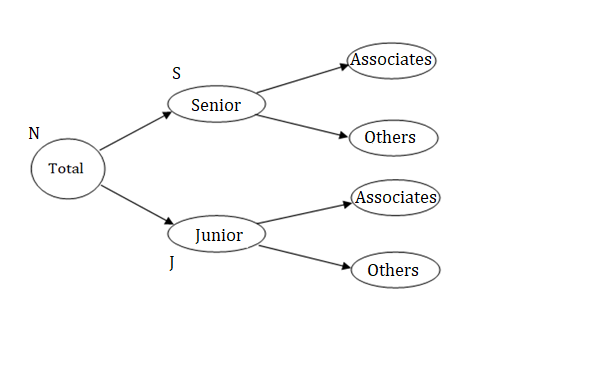
We need to account for one more division, that is the senior and junior associates, who are male and female.

Let us assume that,

• The number of senior associates = A_S, and the number of junior associates = A_J
• The number of senior associates, who are male = M₁ and number of senior associates, who are female = F₁
• Similarly, the number of junior associates, who are male = M₂ and number of junior associates, who are female = F₂

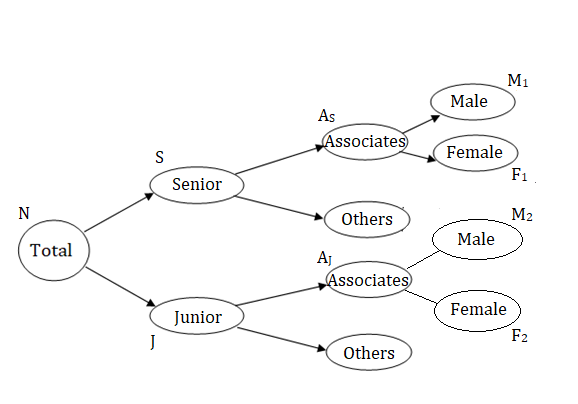
Establish Relations

The next step is to establish a relation between each and every branch with its stem.

Before, that let’s see what we are asked to find out: “what percentage of the junior associates, in the firm, are male”

• From the diagram, we can see that the number of junior associates, who are male is represented by M₂
  • Therefore, we need to find the value of (M₂/A_J) * 100, where A_J = M₂ + F₂

Now that we know the expression, for what to be found, let’s move further.

Note that we can find the value of (M₂/A_J) * 100, if we know the values of M₂ and F₂ (or) M₂ and A_J.

• Let’s start with the trunk, that is the total number of employees in the firm
• From the diagram, we can see that the total number of employees in the firm = the number of senior employees(S) + the number of junior employees(J)
  • N = S + J ……… (1)
• And from the given information, we know that S = N/4 ………. (2)
• Solving equations (1) and (2), we get
  • S = N/4 , and J = 3N/4

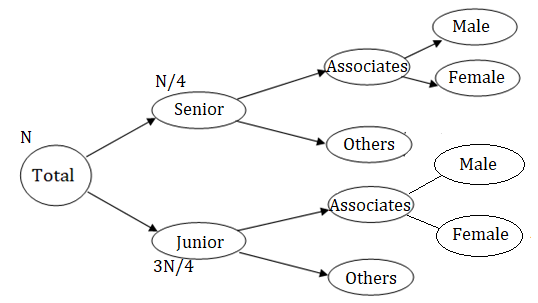
Now that we know the fraction of senior and junior employees in the firm, let’s move further to find how many of the senior and junior employees are associates.

• From the given information, we can infer that,
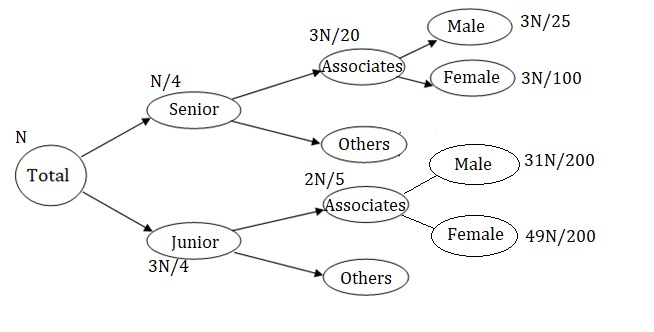
  • A_S = 60% of S = 6S/10 = 6/10 * N/4 = 3N/20
  • A_J = 40% of N = 4N/10 = 2N/5

Now, let’s use the given information to establish more relations

• “80% of the senior employees, who are associates, are male,”
  • Let’s translate this statement into a mathematical equation,
  • From the diagram, we can see that the number of senior employees, who are associates = A_S
    • Thus, 80% of A_S = (8/10) * (3N/20) = 3N/25 = M₁ ……………. (3)
• From the diagram, we can see that, A_S = M₁ + F₁ = 3N/20
  • Thus, F₁ = (3N/20) – (3N/25) = 3N/100
• “Total number of male associates is equal to the total number of female associates”
  • From the diagram, we can see that,
    • Total number of male associates = M₁ + M₂
    • Total number of female associates = F₁ + F₂
• This implies, M₁ + M₂ = F₁ + F₂
• Substituting the values of M₁ and F₁, we get,
  • (3N/25) + M₂ = (3N/100) + F₂
  • Thus, F₂ – M₂ = (3N/25) – (3N/100) = 9N/100 …………. (4)
  • And, we know, A_J = F₂ + M₂ = 2N/5 …………. (5)
• Solving equations (4) and (5), we get,
  • (4) + (5) gives, 2F₂ = (2N/5) + (9N/100) = 49N/100
  • Implies, F₂ = 49N/200
  • Thus, M₂ will be (2N/5) – (49N/200) = 31N/200

Therefore, M₂/J * 100 = (31N/200)/( 2N/5) * 100 = (155/4)%

Important Takeaways

• Tree structures help us to summarize and visualize all the information given in the question by representing all the possible cases by a set of branches, emanating from the main stem, which is labeled according to the given information.
• The sum of values of all the branches must be equal to the sum of its stem value.
• In questions related to percent’s, we do not need the stem value to find the percentage value of any branch or sub-branch, if we have a sufficient number of relations between them

Want to read more articles like this?

Now, if you liked this article, then I am sure that you want to read some more articles like this, click here to read all quant articles.

You will also get a lot of practice questions to learn from.

Happy learning and in case of any other GMAT related queries, please write to us at acethegmat@e-gmat.com.

If you are planning to take the GMAT, we can help you with a personalized study plan and give you access to quality online content to prepare. Write to us at acethegmat@e-gmat.com. We are the most reviewed GMAT prep company on gmatclub with more than 2400 reviews and are the only prep company that has delivered more than 700+ scores than any other GMAT club partner. Why don’t you take a free trial and judge for yourself?