
Do you feel overwhelmed while learning a plethora of GMAT Geometry formulas and concepts? Do you feel Geometry is your weak topic? You are not alone. Many test takers avoid solving GMAT Geometry questions, as most of them don’t feel comfortable with this topic.
In this article, you will read-
- Why is GMAT Geometry your weak area?
- How will we help you improve Geometry?
- Basic properties of triangles for GMAT Geometry
- Illustrative examples showing usage of GMAT Geometry Formulas
- Takeaways

- There are too many GMAT Geometry formulas to remember. Even though GMAT tests us on a very limited number of properties, but since these limited properties are not collated in a single place, it is difficult for a test taker to confidently say he knows all the concepts.
- And say, even if someone manages to find and learn all the concepts, most of them are not sure how to apply these concepts to deduce information from the given question and figure in the questions tested on the GMAT.
NOTE: This is the second article in our GMAT Geometry Pitfalls series. Do read the first article click on the link below.
Most common mistakes in GMAT Geometry Questions
The next 2 articles in this series are:
How will we help you with GMAT Geometry Prep?
In this article, we will address both the above issues by:
- Consolidating the MOST important GMAT Geometry concepts needed in Triangles.
- Focusing on some GMAT-like and official questions and illustrating the application of the above concepts in these questions.
Basic properties of triangles
This section covers the following aspects:
- Finding if a set of given numbers could be the lengths of a triangle or not
- The range of values the side of a triangle can take given the values of the other two sides, and
- The properties of the angles of the triangle
Concept 1: GMAT Geometry formulas
Geometry GMAT Concept 1 – Sum of lengths of any two sides of a triangle > Length of the third side
Suppose you are given three lengths a, b, and c, and asked to find out if we can form a triangle using these three lengths.
How are you going to approach this problem?
Theory:
To determine if the three lengths will form a triangle or not, we need to know the most basic property of a triangle:
Sum of lengths of any two sides of a triangle > Length of the third side
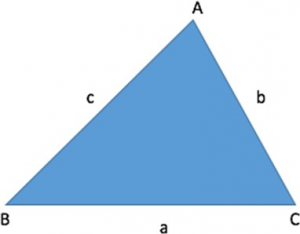
This means that:
- a + b > c
- b + c > a
- c + a > b
Please note that all the three inequalities should satisfy for the triangle to exist.
Let us understand this with the help of a very basic GMAT-like question:
Illustrative Example 1
Q. The three lengths 5, 3, and x are used to form a triangle. Which of the following can be the value of x?
- 6
- 9
- 10
- 12
- 14
Since 5, 3 and x form a triangle, they must satisfy the property –
Sum of lengths of any two sides of a triangle > Length of the third side
Therefore, we can write –
I. 5 + 3 > x II. 3 + x > 5 III. 5 + x > 3
=> x < 8 => x > 2 => x > -2
we can conclude that the range of x is: 2 < x < 8
Out of the given options, the only option that falls within this range is 6. Hence, option A is our answer.
Therefore, now we know:
- How to find if the given lengths form a triangle or not
- How to use the above property to find the range of values for an unknown side in a triangle
Concept 2: GMAT Geometry Formulas
Suppose after finding out that the given lengths form a triangle, you want to find out how the length of the sides can help in finding a relation between the angles of the triangle.
To understand this, we need to know two more important properties:
GMAT Geometry Concept 2 – The sum of the interior angles of a triangle is constant and is equal to 180°
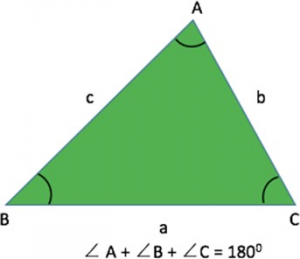
Please note that the above property holds true for all triangles irrespective of their size and shape.
(Notice I am using capital A, B and C to denote the angles of the
triangle and a, b, and c for the lengths of the sides of the triangle)
Property 3 – In any triangle, the largest side is always opposite the largest angle and the smallest side is always opposite the smallest angle
Let me explain this a bit more in detail:
If ABC is a triangle, in which we know that the lengths AB, BC, and CA follow the relation AB>BC>AC, then we can conclude that, since AB is the greatest side the angle opposite to it i.e., angle ACB is the greatest angle.
And since BC > AC, angles opposite to them also hold the same relation, that means angle BAC > angle ABC
Hence we can conclude that: ∠ ACB > ∠ BAC > ∠ ABC
Keep in mind that the converse is also true, i.e., if the relation between the angles is given, we can use that to find the relation between the sides.
The devil is in the details! Planning out the finer details of your study schedule takes you one step closer to your target GMAT score. Learn the other benefits of a well defined study plan in this article.
Save 60+ hours of GMAT preparation by crafting a well-defined study plan in just 3 steps:
Let us understand the application of this property through an example:
Illustrative Example 2
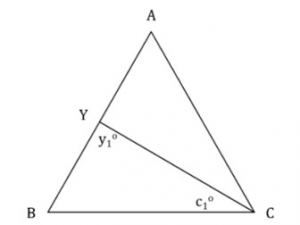
In the triangle given below, all the points denoted are non-overlapping and the angles A, B, and C are distinct. Is AB > AC > BC?
- ∠ y1 = ∠ c1
- ∠ BAC < ∠ ABC and neither angle is the greatest in the triangle ABC
Solution:
Approach
We need to find if the statement AB > AC > BC is true or not. For this, it is enough to get a relation among angles A, B and C since the sides of a triangle follow the same relation as the angles opposite to them.
Analyze Statement 1
∠y1 = ∠c1
Therefore, in ΔBYC
BY = BC
But AB = BY + YA
AB > BC
However, we cannot infer any relationship between BC and AC (or AB and AC) from the given information
Analyze Statement 2
Given ∠ BAC < ∠ ABC and neither angle is the greatest.
Also, in the question statement, it is mentioned that angles BAC, ABC, and ACB are distinct, therefore, ∠ACB has to be the greatest angle.
Therefore, we can conclude, ∠ BAC < ∠ ABC < ∠ ACB
Thus, we can conclude that length BC < AC < AB
Hence, statement 2 is sufficient to arrive at a unique answer.
Correct Answer: B
Takeaways – Article 1 – GMAT Geometry Triangle Concepts
This brings us to the end of the first article in this series. I hope you find it useful and informative. After reading this you should be able to easily:
- Apply GMAT Geometry Concept 1, to identify if a triangle can be formed from the given three lengths
- Apply GMAT Geometry Concept 1, to also find the range of the unknown side, if the other two lengths of the triangle are given
- Apply GMAT Geometry Concept 2 in questions where the relation of angles and sides are required to solve the problem
Keeping these takeaways in mind, can you solve the 2 questions?
- Mastering Important Concepts Tested By GMAT in Triangles – Exercise Question #1
- Mastering Important Concepts Tested By GMAT in Triangles – Exercise Question #2
If you are planning to take the GMAT, we can help you with a personalized study plan and give you access to quality online content to prepare. Write to us at acethegmat@e-gmat.com. We are the most reviewed GMAT prep company on gmatclub with more than 2400 reviews and are the only prep company that has delivered more than 700+ scores than any other GMAT club partner. Why don’t you take a free trial and judge for yourself?
In the next articles on Triangles, read about
1. Tabular Representation: Different types of triangles with their MOST important properties.
2. Special Properties: A few special properties that can be tested by GMAT.
[1] Formulas is the plural form of formula, the alternate plural of formula is formulae.












