A 7 min read

GMAT Inequalities has been the Achilles’ heel for many test takers aspiring to score high in GMAT Quant (Q50 – Q51),  It has sent many test takers on the path of ‘not-so-good’ scores. Therefore, our GMAT Quant Subject Matter Experts have created this article, so that you can learn to solve GMAT Inequalities questions well and get a great score, read Q51.

In this article, we will help you solve the GMAT Inequalities questions by learning the Wavy Line Method. The article talks about the following:

• Introduction to Wavy Line Method – How to Solve GMAT Inequalities Questions
• Wavy line method application – Multiple instances of the same root
• How to draw the wavy line?
• Food for Thought – GMAT inequality questions
• Using wavy line to solve the inequalities questions
• What if an Algebraic expression contains an expression?
• Takeaway – GMAT Inequalities Questions
• Practice & Sample Problems with Solutions on GMAT Inequalities Questions

Guillermo scored a Q50 and got an admit from the Wharton School . In his amazing success story he talks about how he managed his work and preparation with a rock-solid study plan.

How to solve GMAT Inequalities Questions – Wavy Line Method

Wavy Line Method also called the method of intervals is used to solve inequalities containing algebraic expressions in a single variable. This method helps to identify the range of values satisfying an inequality.

For instance, consider the following question:

Find the range of values of x satisfying the inequality (x – 3) (x – 6) < 0.

To solve this inequality, you draw the wavy line as follows:

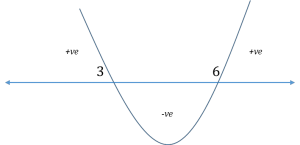
And your inferences regarding the expression (x – 3)(x – 6) would be:

1. The expression will be positive for the range of values for which the curve is above the number line.
   • In the above example, the pertinent ranges are x < 3 and x > 6. So, any value of x either less than 3 or greater than 6 will make the above expression positive in
2. The expression will be equal to zero for the values at which the curve intersects the number line.
   • In the above example, the pertinent points are x = 3 and x = So, both these values make the expression zero.
3. The expression will be negative for the range of values for which the curve is below the number line.
   • In the above example, there is only one portion where the curve is below the number line and this portion corresponds to the range 3 < x < 6. So, any value of x strictly between 3 and 6 will make the above expression negative in

For any strategic advice for GMAT or MBA Admissions, write to us at acethegmat@e-gmat.com. 

Since the above question asks for the range of values of x for which the expression is negative, the answer would be 3 < x < 6.

Well, that was a simple question, so the application of the wavy line method was fairly straight-forward.

Now, for many test takers, things can seem complicated as exponents and algebraic fractions are added into the mix. However, the application of this method is pretty straightforward in such scenarios too. Further, we’ll be focusing on such complex application of the wavy line method and list out the two fundamental rules that are used to draw the wavy line to solve any inequalities testing such algebraic expressions on the GMAT.

(This article benefits those who are not familiar with the wavy line method. The rules provided in this article are generic and can be utilized for all cases)

Wavy Line Method Application – Multiple Instances Of The Same Root

Try to solve the following inequality using the Wavy Line Method: (x−1)²(x−2)(x−3)(x−4)³<0

Did you notice how this inequality differs from the example above? Notice that two of the four terms had an integral power greater than 1. How to draw the wavy line for such expressions?

Let me directly show you how the wavy line would look and then later on the rule behind drawing it.

To know how you did, compare your wavy line with the correct one below.

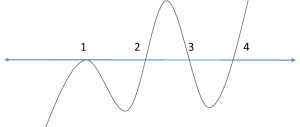
Notice that the curve bounced down at the point x = 1. (At every other root, including x = 4 whose power was 3, it was simply passing through them.)

Can you figure out why the wavy line looks like this for this particular inequality?

(Hint: The wavy line for the inequality (x−1)38(x−2)57(x−3)15(x−4)27<0 is also the same as above) Come on! Give it a try.

If you got it right, you’ll see that there are essentially only two rules while drawing a wavy line.

Remember: We’ll refer to the region above the number line as positive region and the region below the number line as negative region.

What do you need before drawing the wavy line?

1. You need to draw a horizontal line – this will be our Number Line to identify the
2. Mark the “zero points”: Note the values at which at least one of the factor terms in the expression becomes zero.
   • Eg: For instance, in the above expression, x – 1 = 0 at the point x = 1, x – 2 = 0 at the point x = 2, and so on. So, we need to mark the points 1, 2, 3, and 4 on the number line.

How To Draw The Wavy Line?

1. How to start: Once you draw the number line and mark the zero points on the number line, it’s time to draw the wavy line. Start from the top rightmost portion. Be ready to alternate (or not alternate) the region of the wave based on how many times a point is a root to the given

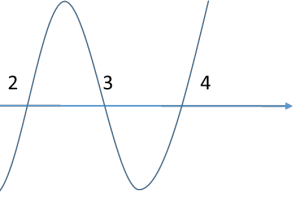
2. How to alternate: If the power of a term is odd, then the wave simply passes through the corresponding point (root) into the other region (to –ve region if the wave is currently in the positive region and to the +ve region if the wave is currently in the negative region).

For instance, in the above example, observe the behavior of the wave at the points 2, 3, and 4.

However, if the power of a term is even, then the wave bounces back into the same region. Observe the behavior of the wave at the point x = 1 (the term (x-1) has an even power in the above expression)

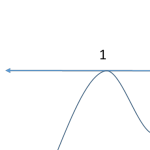
Now look back at the above expression and analyze your wavy line. (Refer to the complete wavy line provided above if required)

Using Wavy Line to Solve the Inequality | GMAT Inequality Questions

Once you get your wavy line right, solving an inequality becomes very easy. For instance, for the above inequality, since we need to identify the range where the above expression would be less than zero, look for the area(s) in your wavy line diagram where the curve is below the number line.

So the correct solution set would simply be {3 < x < 4} U {{x < 2} – {1}}

In words, it is the Union of two regions – region1 between x = 3 and x = 4 and region2 which is x < 2, excluding the point x = 1.

Sign up for a free trial and get unlimited access to concept files, live sessions, and practice questions.

Food For Thought – GMAT Inequalities Questions

Now, try to answer the following questions:

1. Why did we exclude the point x = 1 from the solution set of the last example? (Easy Question)
2. Why do the above-mentioned rules (especially rule #2) work? What is/are the principle(s) working behind the curtains?

What If The Algebraic Expression Contains A Fraction?

Consider the following inequality.

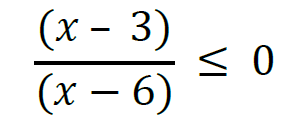
How would you apply the wavy line method to solve the above inequality? The good news is it’s still the same process!

• Draw the number line
• Mark the zero points
• Draw the wavy line per the above rules. However, we need to keep in mind, the following

1. The inequality asks for “≤ 0” (less than or equal to) and not just “< 0” (less than)
   • This is an indicator that the required range is a combination of two ranges: range of

values of x satisfying “ (x-3)/(x-6) < 0” and the values of x satisfying “(x-3)/(x-6) = 0”.

2. The term (x – 6) is in the denominator and we know that we should never consider cases where the denominator becomes zero in any fraction

• So, we need to exclude the point x = 6 out of our solution set.

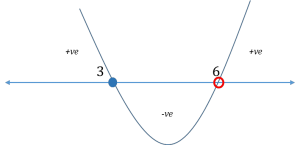
So our solution set becomes 3 ≤ x < 6

(Once again, observe that the point x = 3 is included in the solution while x = 6 is excluded since the term (x-6) is in the denominator)

Get an accurate assessment of your current Quant Ability by attending our Quant Workshop. You’ll get personalized feedback from Our Subject Matter Experts and actionable insights to reach your target Quant score.

Takeaway – Solving GMAT Inequalities Questions using the Wavy Line Method

The approach to solving an algebraic inequality using wavy line method is two-part:

Drawing the Wavy Line:

• Draw the Number Line
• Mark the Zero Points
• Start from the top right portion and draw the wavy line
  • If a term has odd power, the wavy line passes through the corresponding zero point
  • If a term has even power, the wavy line bounces off the corresponding zero point

Identifying the correct range of values:

• On the basis of the sign of the expression required, identify the pertinent regions of the wavy line
  • The region(s) above number line = Value of expression will be positive
  • Intersection points = Value of expression equal to zero
  • The region(s) below number line = Value of expression will be negative 

For further reading on GMAT Number Properties concepts & questions, follow our articles on Even-Odd Properties and LCM-GCD Questions. 

Foot Note: Although the post is meant to deal with GMAT inequality expressions containing multiple roots, the above rules to draw the wavy line are generic and are applicable in all cases.

GMAT Inequalities Questions – Exercise Problems with Solutions

Here is a list of GMAT inequalities questions specifically designed to help you apply the learnings from this article:

Question 1

Question 2

Question 3

Question 4

Question 5

Question 6

Question 7

---

Having gone through this article, you should now be able to solve any of the GMAT Inequalities questions using the Wavy Line Method. Good luck with your preparation!