Homepage > GMAT Preparation > GMAT Quant > Geometry > Quadrilateral questions and solutions

Quadrilateral questions and solutions

Posted by Ashutosh | Sep 24, 2019 | Geometry, GMAT OG Solutions, GMAT Preparation, GMAT Quant, Quant OG Solutions

A 11 min read

Quadrilateral questions have always been a head-scratcher for a lot of candidates taking competitive or standardized exams. The primary reason behind it is learning a concept is easier as compared to applying that concept to solve questions.

Therefore, to help you with the application of properties of quadrilaterals we have shared a few quadrilateral questions and solutions in this article.

Here is the outline of this article:

Questions on Rectangles
Questions on Squares
Questions on Rhombus
Questions on Parallelogram
Questions on Trapezium

Rectangle

Question 1

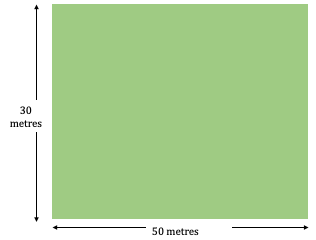
What is the area of a field that is in the shape of a rectangle having dimensions 30 meters and 50 meters?

80 sq. metres
160 sq. metres
1500 sq. metres
1600 sq. metres
3000 sq. metres

Solution

Given and to find:

We are given the dimensions of the rectangular field as 30 metres and 50 metres and

We need to find its area.

Approach

We know that field is rectangular in shape. Hence, we can apply the area of rectangle to find the field area.

Length of the field = 50 Metre
Width of the field = 30 Metre

Area of the rectangular field = Length × Width = 50 × 30 = 1500 Sq. Metres

Hence, option C is the correct answer.

Properties and formulas Used in this question

Area of the Rectangle = Length × Width

From the above list, we can see that we used only one simple property to find the answer.

Now, let’s see one variation of this question that is GMAT-like.

Question 2 – GMAT Like

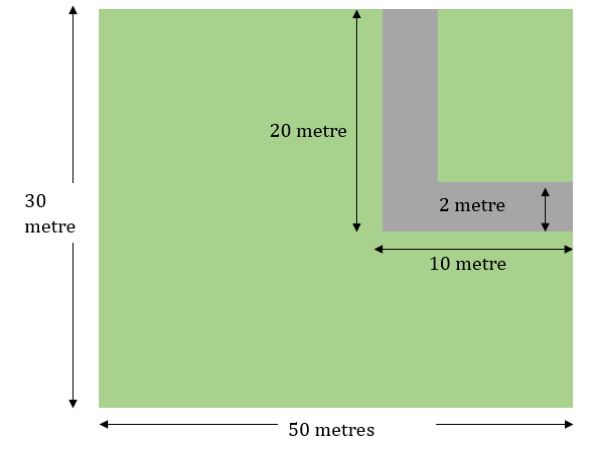
A pathway having uniform width of 2 metres was made in a rectangular field. What is the area of the field excluding the path if the dimensions of the field are 30 meters and 50 meters?

1100 sq. metres
1300 sq. metres
1400 sq. metres
1444 sq. metres
1460 sq. metres

Solution

Given and to Find:

We are given:

A pathway has a uniform width of 2 metres.
It was made in a rectangular field.
The filed has dimensions 30 meters and 50 meters.

We need to find:

The area of the field excluding the pathways.

Approach

We can get the area of the field excluding the pathways if we subtract the area of the pathway from the area of the field.

Area of the field excluding the pathways = Area of the field – Area of the pathway.
- Area of the field = 1500 sq. meter
- However, pathway is not a rectangle
  - But we can break the pathway in to three parts as shown below and get three rectangles

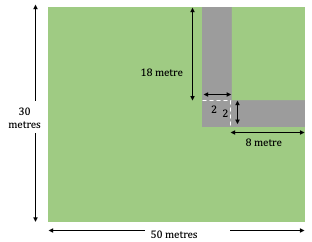
Hence, area of the pathway = Area of (Rectangle of size 18 × 2 + Rectangle of size 2 × 2 + Rectangle of size 8 × 2)

= 18 × 2 + 2 × 2 +8 × 2
= 36 +4+ 16 = 56 sq. meter

Thus, Area of the field excluding the pathways = 1500 – 56 = 1444 sq. metres

Properties and formulas Used in this question

Area of the Rectangle = Length × Width

In this question, the process used is also same. But we have to visualize that pathway can actually be broken into 3 separate rectangles. And, this further simplifies the calculation.

Square

Question 1

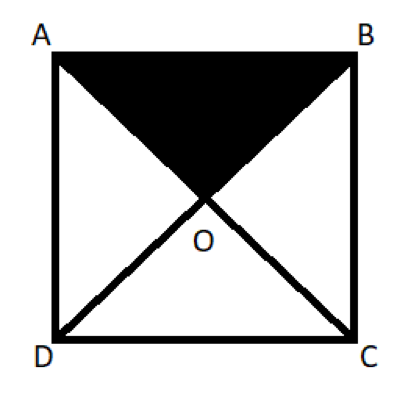
In a square ABCD, the diagonals intersect at a point O. If the side length of the square is 4 units, then what is the area of the shaded region?

Solution

Given

In this question, we are given a square ABCD with a side length of 4 units, and the diagonals of the square intersect at a point O.

To find

With this information we are asked to find out the area of the shaded region, that is triangle AOB

Approach

Alright, before we head to solve this question, let’s just recall a useful property of squares from the article, that is the diagonals, in a square, bisect each other at right angles.

Now, tell me, what are the angles in each of these four triangles?
- The angles in all four triangles are 45-45-90, right?
  - Since all the angles in a square are 90 degrees and the diagonals bisect those angles.
  - And the angles at the center of the square are all right angles
So, we can say that the diagonals divide the square into four isosceles right-angled triangles, which are congruent.
Now, most of you might think how are they congruent?
- If we observe the given diagram, we can see that
  - The hypotenuse of all the triangles is nothing but the side of the square
  - And, since the diagonals bisect each other, in a square, OA = OB = OC = OD
  - Thus, all four triangles have same side lengths, hence they are congruent triangles
  - Since the triangles are congruent their areas are also equal

With this information, let’s try to establish a relationship between area of the square and area of triangle AOB.

We can say that the area of the square = area of AOB + area of BOC + area of COD + area of DOA = 4 * area of AOB (since the areas of triangles are equal)
Therefore, area of AOB = area of the square/4 = 4 * 4/4 = 4 sq. units

Hence, the correct answer is Option B.

Properties and formulas Used in this question

All the sides of a square are equal.
All its internal angles are 90⁰.
Area of the square.
The diagonals in a square bisect each other at right angles
The diagonals in a square divide the square into four congruent isosceles right-angles triangles

From the above list, we can see that we used the above properties/formulas to easily answer the question.

Now, let’s see one variation of this question that is GMAT-like.

Question 2

If the length of one of the diagonals of a square is p units, then what is the perimeter of the square?

√2p
2p
2√2p
4p
4√2p

Solution

Given and to find

In this question, it is given to us that:

length of one of the diagonals of a square is p units, and we need to find:
The perimeter of the square.

Approach

Now, do we know what is the perimeter of the square?
- Yes, we do. It is the sum of all the sides.
And, all the sides of a square have the same length.
Hence, perimeter of square = 4 times the side length
- Therefore, once we have the side length, we can find our answer.

However, we are only given the length of one of the diagonals of the square and not the side length.

Can we find the side length using this information?
Let us try to find it out.

Let’s recall a useful property of squares from the article, that is all the interior angles in a square are right angles, 90 degrees.

If all the sides are equal and all the angles are equal, then by applying the Pythagoras theorem, we can say both its diagonal will also be equal.

Now, let’s try to visualize a square with one diagonal joined. We can clearly notice that the diagonal divides the square into two right triangles, and the diagonal is the hypotenuse.

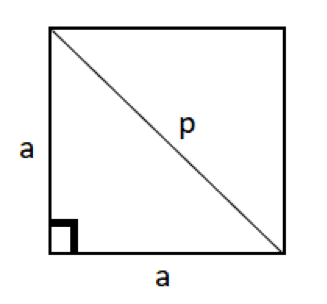
Thus, applying the Pythagoras rule, we can say that,

Side₁² + Side₂² = Diagonal ²
a² + a² = p²
2a² = p or a² = p²/2
- From this we get the length of the side as p/√2 units

Therefore, the perimeter of the square = 4 * (p/√2) = 4 * (p/√2) * (√2/√2) = 2√2p units

Hence, the correct answer is Option C.

Properties and formulas used in this question

All the sides of a square are equal.
All its internal angles are 90^°.

Pythagoras theorem
Perimeter of the square.

From the above list, we can see that we used the above properties/formulas to easily answer the question.

Rhombus

Question 1

If the lengths of two diagonals of a rhombus are 6 and 8 units, then what is the perimeter of the rhombus?

Solution

Given

In this question, we are given a rhombus, with diagonal lengths 6 and 8 units

To find

With this information, we are asked to find out the perimeter of the rhombus

Approach

Alright, before we head to solve this question, let’s visualize the given information in the form of a diagram.

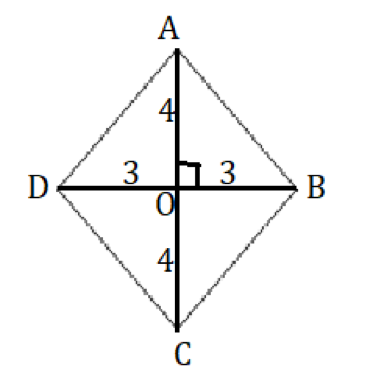
Because we know that the diagonals in a rhombus bisect each other at right angles.

In triangle AOB, applying Pythagoras rule, we get

AB² = AO² + OB²
AB² = 3² + 4²
9 + 16 = 25
Thus, AB = 5 units

This implies, AD = BC = CD = 5 units.

Since, in a rhombus, all sides are equal.

Therefore, the perimeter of rhombus = 4 * 5 = 20 units

Hence, the correct answer is Option C.

Properties and formulas Used in this question

All the sides of a rhombus are equal.
The diagonals bisect each other at right angles.
Pythagoras rule

From the above list, we can see that we used the above properties/formulas to easily answer the question.

Now, let’s see one variation of this question that is GMAT-like.

Question 2 – GMAT like

In a rhombus ABCD, if the length of side BC is 1 unit and the value of interior angle A is 60^o, then what is the length of its shorter diagonal?

1
√3
2
2√3
Cannot be determined

Solution

Given and to find

In this question, it is given to us that:

In a rhombus ABCD, BC = 1 unit
Angle A =60^o

With this information, we are asked to find

The length of the shorter diagonal

Approach

Alright, before we head to solve this question, let’s visualize the given information in the form of a diagram

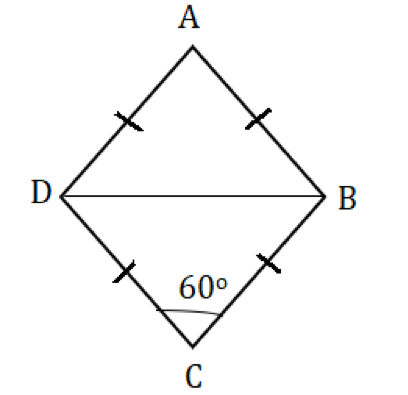
In triangle BCD, angle DBC = angle CDB = 60 degrees

Because we know that the BC + CD (sides of rhombus)
Thus, BCD is an equilateral triangle and BD = BC = 1 unit

Let us also find the length of the other diagonal, because we do not know which one is shorter yet.

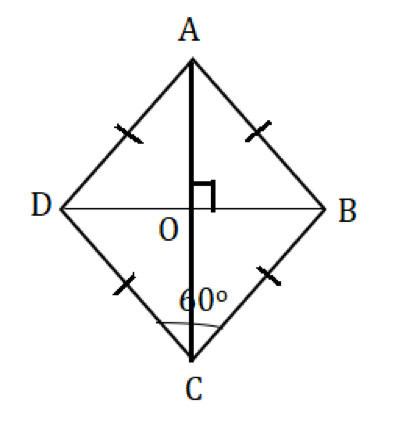
The length of other diagonal = AC = AO + OC = 2OC (since the diagonals bisect each other)

To find OC, let us consider triangle BOC.

Now, tell me, what are the angles in this triangle?
- 30-60-90, right?
Thus, the sides of triangle BOC must be in the ratio 1:√3: 2 respectively
We know BC = 1, which implies OC = √3/2

Therefore, AC = √3 units, which is greater than BD = 1 unit

Hence, the correct answer is Option A.

Properties and formulas Used in this question

All the sides of a rhombus are equal.
The diagonals bisect each other at right angles.
The ratio of sides in a 30-60-90 triangle
All the sides of an equilateral triangle are equal

From the above list, we can see that we used the above properties/formulas to easily answer the question.

Parallelogram

Question 1

If the sum of lengths of two adjacent sides of a parallelogram is 5 units, then what is the perimeter of the parallelogram?

Solution

Given

In this question, we are given a parallelogram, in which the sum of the lengths of two adjacent sides is 5 units.

To find

With this information, we are asked to find out the perimeter of the parallelogram

Approach

Alright, this question is quite simple, if you can apply the property of a parallelogram.

Let’s see what is that property.

Firstly, let us assume that the lengths of four sides as a, b, c and d units as shown below

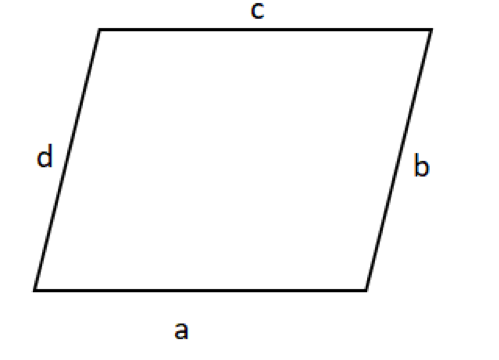
Therefore, the perimeter = a + b + c + d

Now, tell me, what is the relation between a and c?

They both are equal, right?
Since, in a parallelogram opposite sides are parallel and equal.
Thus, a = c and b = d
This implies, perimeter = a + b + a + b = 2 * (a + b)
And, we are given that the sum of two adjacent sides is5units, that is a + b = 5 units
Therefore, the perimeter of the given parallelogram = 2 * 5 = 10 units

Hence, the correct answer is Option A

Properties and formulas Used in this question

Opposite sides of a parallelogram are equal.
Perimeter of a parallelogram

From the above list, we can see that we used only one simple property to find the answer.

Now, let’s see one variation of this question that is GMAT-like.

Question 2 – GMAT like

The area of a parallelogram which has all sides of equal length is 1 sq. units. If one of the interior angles of a parallelogram is 30 degrees, then what is the perimeter of the parallelogram?

1
√2
2√2
4√2
Cannot be determined

Solution

Given and to find

In this question, it is given to us that:

The area of a parallelogram = 1 sq. units
All sides are of equal length, let us assume it as p units, and
One of the interior angles = 30 degrees

With this information, we are asked to find

The perimeter of the parallelogram = p + p + p + p = 4p units

Approach

Firstly, let us try to visualize all the given information

Now, tell me, how can we find the value of p?

The only information that we are left with is the area of the parallelogram, so let’s try to use it
Let us drop a perpendicular from the top vertex tn the base of the parallelogram

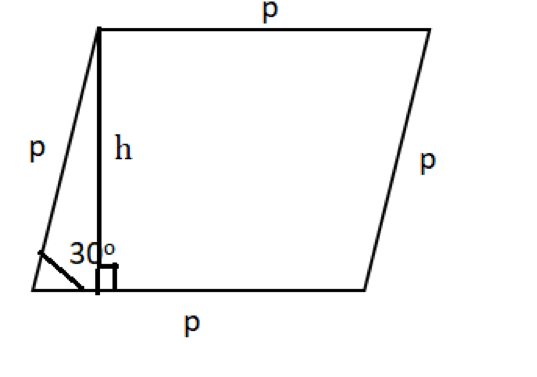
Now, observe the triangle that is formed, it is a 30-60-90 triangle.

And we know that the sides of a 30-60-90 triangle will be in the ratio 1:√3: 2 respectively
- So, the height of the parallelogram, h = p/2
Also, we know that the area of the parallelogram = base * height = p * p/2 = p²/2, which is equal to 1 sq. unit
- Thus, we get the value of p =√2 units
Therefore, the perimeter of the parallelogram = 4√2 units

Hence, the correct answer is Option D.

Properties and formulas Used in this question

Area of a parallelogram.
Perimeter of a parallelogram.
The ratio of sides in a 30-60-90 triangle

From the above list, we can see that we used the above properties/formulas to easily answer the question.

Trapezium

Question 1

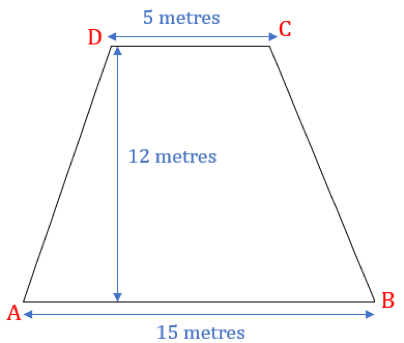
What is the area of the below-shown trapezium ABCD?

75 sq. metres
100 sq. metres
120 sq. metres
200 sq. metres
240 sq. metres

Solution

Given and to Find

We are given a trapezium ABCD and we need to find its area.

We are also given:

Length of opposite parallel sides = 15 and 5 meters
Height of the trapezium = 12 metres

Approach

We can directly apply the area of the trapezium formula to find the answer.

Area of trapezium= ½ × (Sum of parallel sides) × Height = ½ × (5 + 15) × 12= 120 sq. metres

Hence, the correct answer is option C.

Properties and formulas Used in this question

Area of the trapezium = ½ × (Sum of parallel sides) × Height

We used only one simple property to find the answer. Now, let’s see one variation of this question that is GMAT-like.

Question 2 – GMAT like

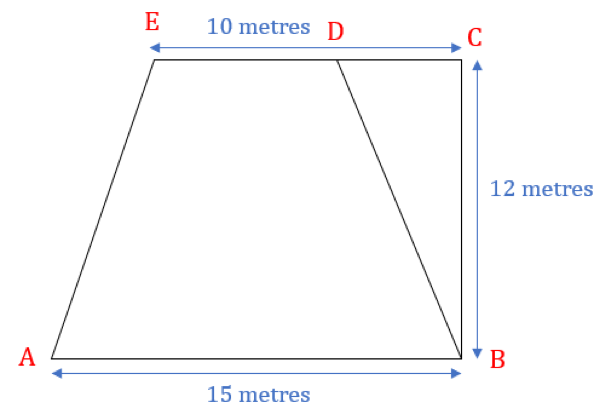
What is the area of ABED if AB is parallel to CE and BCD is a right-angled triangle at B having area 30 square metres?

75 sq. metres
100 sq. metres
120 sq. metres
200 sq. metres
240 sq. metres

Solution

Given and to find:

We are given:

AB is parallel to CE.
BCD is a right-angled triangle at B.
Area of triangle BCD = 30 sq. meters

We need to find:

Area of ABED

Approach

ABED is trapezium. But we cannot apply the area of trapezium formula here as we are not given the length of DE.

So, let us see how we can find DE.

DE = CE – CD = 10 – CD.
- Now, if we find CD then we can find the answer.
Let us see if we are given any information related to CD.
CD is the part of a triangle BCD and its area is 30.
- 30 = ½ × BC ×DC
- 30 = ½ × 12 ×DC
- DC = 5

Thus, CD = 5 meter.