The primary objective of this article is to cite 3 most common mistakes made by students while solving GMAT rate problems on Time Speed Distance. To make sure you understand each common mistake we’ll use illustrative GMAT rate problems on Time Speed Distance.
The key highlights of this article are –
- Common Mistake 1 – GMAT Rate Problems – Time Speed Distance
- Common Mistake 2 – GMAT Rate Problems – Time Speed Distance
- Common Mistake 3 – GMAT Rate Problems – Time Speed Distance
- Takeaways from this article
This is the second article of the series on Time, Speed and Distance. We would strongly suggest you to read the first article on the application of Average Speed in Distance Problems.
Common mistake 1| Incorrect or missing unit conversion | GMAT Rate Problems
Example 1
During a certain time period, Car X traveled north along a straight road at a constant rate of 1 mile per minute and used fuel at a constant rate of 5 gallons every 2 hours. During this time period, if Car X used exactly 3.75 gallons of fuel, how many miles did Car X travel?
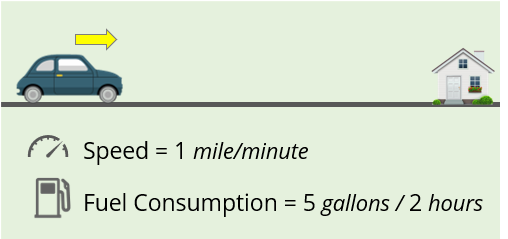
Solution
Common approach used by students – 1
In this question, we need to find out how many miles did Car X travel.
To find the distance covered, we have the following information given:
- The Car used exactly 75 gallons of fuel in this time period
- The Car used fuel at a constant rate of 5 gallons every 2 hours
- Also, the Car travelled at a constant rate of 1 mile per minute
We already know the fuel consumption rate and the total fuel consumption of the car. Therefore, we can divide the total fuel consumption by the rate of fuel consumption to find out the time taken to complete the journey.
- The journey time = 3.75/5 = 0.75 miles
Multiplying the journey time by the speed, we can calculate the distance
- Journey distance = 0.75 × 1 = 0.75 miles
If you have got 0.75 miles as the answer, then you have solved it incorrectly
Let’s see another approach done by students while solving this question:
Common approach used by students – 2
In this question, we need to find out how many miles did Car X travel.
To find the distance covered, we have the following information given:
- The Car used exactly 3.75 gallons of fuel in this time period
- The Car used fuel at a constant rate of 5 gallons every 2 hours
This indicates, the rate of consumption is 2.5 gallons per hour
- Also, the Car traveled at a constant rate of 1 mile per minute
We already know the fuel consumption rate and the total fuel consumption of the car. Therefore, we can divide the total fuel consumption by the rate of fuel consumption to find out the time taken to complete the journey.
- The journey time = 3.75/2.5 = 1.5 hrs
Multiplying the journey time by the speed, we can calculate the distance
- Journey distance = 1.5 × 1 = 1.5 miles
If you have got 1.5 miles as the answer, then you have solved it incorrectly
The mistakes and the correct approach | GMAT Rate Problems
If we observe closely, there has been no difference in terms of the procedures of both the solutions
- Conceptually both the processes are correct. However, the answers are different because of the wrong interpretation of the given values.
Error 1: Given that the Car used fuel at a constant rate of 5 gallons every 2 hours, first we need to calculate the fuel consumption rate per hour.
As the Car used 5 gallons every 2 hours, the rate of fuel consumption (i.e. fuel consumption in every hour) = 5/2 gallons per hour = 2.5 gallons per hour
Therefore, journey time = 3.75/2.5 hrs = 1.5 hrs
Error 2: In the 2nd approach, the rate of fuel consumption has been calculated correctly. But while calculating the distance, the speed of the car is applied incorrectly in both the methods.
- Given that the speed of the car is 1 mile per minute
- It means the speed of the car is 60 miles per hour
We need to convert the speed into miles per hour, as the journey time has been calculated in hours.
In an opposite way, we could have taken the speed in mile per minute also, in that case, we need to convert the total journey time in minutes.
Final Answer: As we have already calculated the speed as 60 miles per hour and the journey time as 1.5 hrs,
- The total distance traveled = 60 × 1.5 miles = 90 miles
Key Takeaways | Common Mistake 1
While considering any of the values of speed, distance, and time for calculation, make sure the units of all of them are same. Otherwise, it will lead to an incorrect calculation.
Speaking of calculation, Do you know how GMAT scores are calculated? Read more to understand GMAT scores.
Common mistake 2 | Calculation of Average Speed, without considering everything into account
Example 2
Last Sunday, Archie visited his friend Veronica who lives 90 miles from his place. He divided his onward and return journey in a different manner. He reached Veronica’s place by dividing the total distance in two equal part, at a speed of 15 mph and 30 mph respectively. He stayed there for 2 hours and took the return journey via the same path by dividing the total journey time into three equal parts, at a speed of 5 mph, 10 mph, and 15 mph respectively. If x, y, and z denote the average speed of his onward, return, and overall journey respectively, what is the value of x + y + z?
Solution

In this question, we need to find out Archie’s average speed in his onward journey, return journey, and his whole journey. For that, we need to know the following:
- Total distance traveled, and the total time taken
- Individual distances for both onward and return journey
- Individual time taken for both onward and return journey
Now as it is given that Veronica lives at a distance of 90 miles from Archie’s place, we can say for the to-and-fro journey, total distance covered = (90 + 90) miles = 180 miles, whereas the individual distances at onward and return journey will be 90 miles each.
As we already have the value of the total distance, we need to find out the total travel time only.
Still unsure of your GMAT Quant preparation? Attend our Quant Workshop to get an accurate assessment of your Quant Ability and precise diagnosis of your weak areas alongwith a defined path to your target GMAT Score.
Common approach used by students – 1:
- In the onward journey, the whole distance is covered in two parts, at a speed of 15 mph and 30 mph respectively.
Therefore, the average speed in the onward journey = (15+30)/2 mph = 22.5 mph
- Similarly, in the return journey, the whole journey time is divided into three equal parts, at a speed of 5 mph, 10 mph, and 15 mph respectively.
Therefore, the average speed of the return journey = (5+10+15)/3 mph = 10 mph
Hence the overall average speed = (22.5+10)/2 mph = 16.25 mph
If you have got 22.5 mph and 16.25 mph as the average speed in the onward journey and overall journey respectively, then you have solved it incorrectly.
Common approach used by students – 2:
It is given that, in the onward journey the distance is divided into two equal parts.
As the total onward journey distance is 90 miles, each part has a distance of 45 miles.
- The first half of 45 miles distance is covered at a speed of 15 mph, therefore, the time taken to cover that distance = 45/15 hrs = 3 hrs
- The second half of 45 miles distance is covered at a speed of 30 mph, therefore, the time taken to cover that distance = 45/30 hrs = 1.5 hrs
Therefore, total journey time in the onward travel = (3 + 1.5) hrs = 4.5 hrs
So, the average speed in the onward journey = 90/4.5 mph = 20 mph
Similarly, in the return journey, the time taken is divided into 3 equal parts.
Therefore, the total time of 4.5 hrs is divided into 1.5 hrs each, which is covered at an individual speed of 5 mph, 10 mph, and 15 mph respectively.
So, the average speed in the return journey = 90/(1.5+1.5+1.5) mph = 20 mph
And, also the average speed of the overall journey = (90+90)/(4.5+4.5) mph = 20 mph
Again, if you have calculated 20 mph as the average speeds, then your answer is incorrect.
The mistakes and the correct approach | GMAT Rate Problems
In both the examples given above, the calculation of average speed is done with some wrong interpretation of the concept and formula. Let us look at the important formula first which are related to average speed, and the conditions applicable to the validity of that formula:
- Average speed = Total distance travelled/ Total time taken to travel that distance
We know that, if the journey distance is divided into two equal parts, with each part is divided in individual speeds a and b respectively, then the overall average speed of the journey = 2ab/(a+b)
Similarly, If the journey time is divided into n number of equal time slots, with each time slot is being covered at different individual speed, then the average speed of the journey is calculated by the arithmetic mean of all the individual speeds.
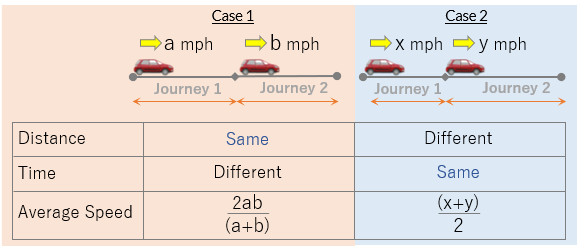
With these understandings, let’s look at the errors mentioned in the demonstrated examples:
Error 1: In the 1st onward journey, the onward distance is covered in two equal journey distances, at a speed of 15 mph and 30 mph respectively. Therefore, the average speed should not be calculated by taking the average of their individual speeds. As per the discussion above, we can calculate the average speed by using the 2ab/(a+b) formula.
Also, one cannot calculate the overall average speed by taking the arithmetic mean of the individual average speeds.
Error 2: Although it was mentioned that the return journey is divided into 3 equal time slots, it was incorrectly assumed that the total time taken in the return journey was same as that of onward journey.
Error 3: While calculating the overall average speed, none of the time the stay time of 2 hours is taken into account.
Final Answer: Rectifying all the errors mentioned above, we can say:
- Average speed in the onward journey = X = (2x15x30)/(15+30) mph = 20 mph
- Average speed in the return journey = Y = (5+10+15)/3 mph = 10 mph
- Total travel time in the onward journey = (45/15) + (45/30) = 3 + 1.5 hrs = 4.5 hrs
- Total travel time in the return journey = 90 x (3/(5+10+15)) hrs = 9 hrs
As Archie had a stay of 2 hours at Veronica’s place, the overall journey time = (4.5 + 2 + 9) hours = 15.5 hours
Therefore, the average speed in the overall journey = Z = 180 / (4.5+2+9) mph = 180/15.5 mph = 11.6 mph
Note that, while calculating the overall average speed, we must consider the 2 hours’ stoppage time also. However, if we consider the onward journey and the return journey separately, we don’t need to consider the stoppage time as there were no stoppages during the onward or journey
Hence, the value of X + Y + Z = 20 + 10 + 11.6 = 41.6 mph
Learn how to avoid 3 mistakes in GMAT Permutation and Combination Questions
Common mistake 3 | Missing the detail information in the question
Example 3
Two buses A and B are of length 15 m and 10 m respectively, and the speed of bus A is 72 kph. If bus A takes 1/2 second to cross the sole passenger sitting inside bus B when they are moving towards each other from opposite direction, find the time taken by bus A to overtake bus B?
Solution
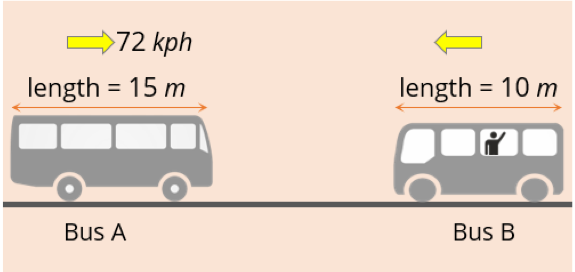
In this question, we need to find out the time taken by bus A to overtake bus B. In order to find that out, we need the following information:
- Length of bus A
- Speed of bus A
- Length of bus B
- Speed of bus B
Now, from the information given in the question, we already have the length of both A and B as well as the speed of A.
- Length of A = 15 m
- Length of B = 10 m
- Speed of A = 72 kph = 20 m/s
Let’s assume the speed of B is x m/s
Common approach used by students:
- It is given that bus A takes 1/2 second to cross the sole passenger sitting inside bus B when they are moving towards each other from opposite direction.
We know that if two bodies are moving from the opposite direction towards each other, their relative speed should be the sum of their individual speed.
- Therefore, the relative speed of bus A and B = (20 + x) m/s
- Distances covered by them = sum of their individual lengths = (15 + 10) m = 25 m
- We know, speed = distance/time
So, we can write, 20 + x = 25/ (1/2)
- Or, 20 + x = 50
Or, x = 30 m/s
- Therefore, the speed of bus B is 30 m/s
If you also have the same value for the speed of bus B, then your answer is incorrect. You have missed a very small detail in the question statement.
The mistakes and the correct approach | GMAT Rate Problems
Error: If you look at the question carefully, you can see it asks the time taken for bus A to overtake bus B. It clearly indicates the speed of bus A must greater than the speed of bus B.
Therefore, the speed of bus B cannot be equal to 30 m/s, as it is already given that the speed of bus A is 20 m/s.
The error lies in the interpretation of the question statement. “If bus A takes ½ second to cross the sole passenger sitting inside bus B…”.
Understand that here bus A is not crossing the whole bus B, but it is only crossing the sole passenger sitting inside bus B. The length of the passenger is negligible compared to bus’s length, but the passenger is moving at the same speed as bus B’s speed.
Therefore, when we are calculating the value of x, we need to consider only the length of bus A, and we do not need to consider the length of bus B.
Hence, the correct equation will be as follows:
- Relative speed of bus A and B = (20 + x) m/s
- Distances covered by them = length of bus A = 15 m
- Speed = distance/time Or, 20 + x = 15/(1/2) Or, 20 + x = 30
Or, x = 10 m/s
Therefore, speed of bus B is 10 m/s
So, the time taken by bus A to overtake bus B = (15+10)/(20-10) sec = 25/10 sec = 2.5 sec
Key Takeaways | Common Mistake 3
Interpretation of every statement given in the question needs to be done very carefully, as not looking into detailing may lead to different results.
The devil is in the details! Planning out the finer details of your study schedule takes you one step closer to your target GMAT score. Learn the other benefits of a well defined study plan in this article.
Save 60+ hours of GMAT preparation by crafting a well-defined study plan in just 3 steps:
Takeaways from the Article | GMAT Rate Problems | Time Speed Distance
- While solving GMAT Rate Problems on Time Speed Distance, one must look into the units of all the given In the question, units may be given in different measures, one must convert all of them in the same measure before doing the calculation.
- While calculating the average speed of a journey, one must consider the stoppage or halt times, if any, within the journey. The final journey time should include all those components of time within the journey.
- While solving GMAT Rate Problems on Time Speed Distance, one must look into the details of the given information. Ignoring details may lead to wrong interpretation of the question stem, which may result in an incorrect answer.
Questions on time, speed and distance are very commonly asked on the GMAT. Ace GMAT Quant by signing up for our free trial and get access to 400+ questions. We are the most reviewed online GMAT Prep company with 2400+ reviews on GMATClub.












