GMAT problem solving questions on Time and Work can be solved easily and quickly provided you do not make mistakes while solving them. In the last article, we compared the conventional methods of solving Time and work questions with the LCM method and the efficiency (work rate) method. If you haven’t read the previous article on how to quickly solve time and work questions we recommend you read that first before going through this article.
Now that you have read and understood the LCM method and efficiency (work rate) method, it’s time to learn about the 3 deadly mistakes and how you can avoid them while attempting Time and Work questions in GMAT Problem solving or data sufficiency.
In this second article of the series on Time and Work, we’ll look
- Objective
- Mistake number 1 – incorrect use of the relationship between efficiency and time taken
- Mistake number 2 – The incorrect approach
- Mistake number 3 – incorrect interpretation of the question statement
- Takeaways
- Practice questions on Time and Work
Objective | GMAT Problem Solving | Time and Work
The primary objective of this article is to cite 3 most common mistakes made by students while attempting Time and Work questions in GMAT problem solving. We will demonstrate them with different examples of each type. For students’ convenience, we have referred to examples similar to what is provided in the official resources.
Mistake number 1 – Incorrect use of the relationship between efficiency and time taken
Let’s understand this mistake with the help of 2 illustrative examples
Example – 1
Six machines at a certain factory operate at the same constant rate. If four of these machines, operating simultaneously, take 27 hours to fill a certain production order, how many fewer hours does it take all six machines, operating simultaneously, to fill the same production order?
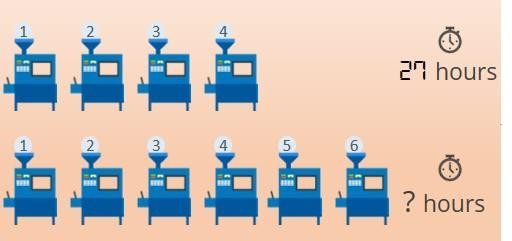
Solution
A common approach used by students:
In this question, it is given that
- 4 machines take 27 hours to fill a certain production order
- All machines operate at the same constant rate
We need to find out the difference in time if 6 machines work on the same production order. Now, it is given that,
- 4 machines take 27 hours to fill the production order
- Hence, 1 machine will take (27/4) hours to fill the same production order
- Therefore, 6 machines will take [(27/4) x 6] hours = 40.5 hours to fill the production order
- Hence, the difference in time taken = (40.5 – 27) hours = 13.5 hours
If you have got 13.5 hours as the answer, then you have solved it incorrectly.
Error in the above approach
In this question, when we are calculating the time taken by 1 machine to complete the production order, we have made a logical error.
It is given that all machines operate at the same working rate.
- Therefore, if 4 machines can fill the production order in 27 hours, logically 1 machine should take 4 times the time taken by 4 machines to fill the same production
- This is happening because the efficiency of 1 individual machine is 1/4 times of the combined efficiency of 4 machines
- Because efficiency and time taken are inversely proportional to each other, the time taken by 1 machine should be 4 times of the time taken by the 4 machines combined
Let us take another similar example
Example 2
Six machines, each working at the same constant rate, together can complete a certain job in 12 days. How many additional machines, each working at the same constant rate, will be needed to complete the job in 8 days?
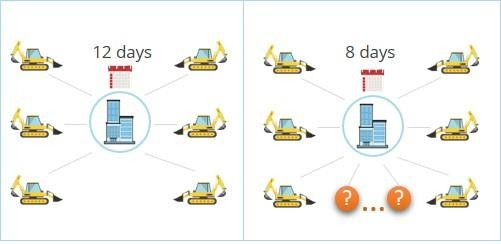
Solution
A common approach used by students:
In this question, it is given that:
- 6 machines can complete a certain job in 12 days
- All machines work at the same constant rate
We need to find out the number of additional machines required to complete the same job in 8 days.
Now it is given that,
- 6 machines can complete the job in 12 days
- Hence, 1 machine can complete the job in 12/6 days = 2 days
- If 1 machine can complete the job in 2 days, we need 8/2 = 4 machines to complete the job in 8 days
If you have got 4 as the answer, then you have solved it incorrectly.
Error in above approach
The solution to this question contains 2 errors.
Error 1: Same as the previous question, if 6 machines can complete the job in 12 days, then 1 machine will be completing it by taking 6 times the original time.
Error 2: Moreover, if 1 machine can complete the job in 2 days, you don’t need 4 machines to complete the job in 8 days – as 1 machine itself can complete it in 2 days’ time.
The Correct Solution
Question 1
Given that,
- 4 machines can complete the job in 27 hours.
- Hence, 1 machine will complete the job in 27 * 4 = 108 hours
- Therefore, the total job is of 108 machine-hours.
- If 6 machines work simultaneously, then they will take 108/6 hours = 18 hours to complete the job
Hence, the fewer hours = (27 – 18) hours = 9 hours
Question 2
Given that,
- 6 machines can complete a certain job in 12 days
- Hence, the total job is of 12 * 6 = 72 machine-hours.
- Now, if the job is supposed to be completed in 8 days, the total number of machines needed to do that = 72/8 = 9
Hence, the additional number of machines required = (9 – 6) = 3
Mistake number 2 – The incorrect approach
To understand how your approach to solving Time and Work questions is incorrect, let’s look at one illustrative example.
Example 3
At his regular hourly rate, Don had estimated the labor cost of a repair job as $336 and he was paid that amount. However, the job took 4 hours longer than he had estimated and, he earned $2 per hour less than his regular hourly rate. What was the time Don had estimated for the job, in hours?
- A) 28
- B) 24
- C) 16
- D) 14
- E) 12
Solution
Information given in the question
This is one of those questions which, if approached incorrectly, can be highly time-consuming and increases the probability of doing it wrong.

In this question, it is mentioned that:
- Don had estimated the labor cost of a repair job as $336, which he was paid
- The job took 4 hours longer than originally estimated
- As a result, Don earned $2 less than his original estimated hourly rate
We need to find out the originally estimated time to finish the job.
A common approach used by students
This question deals with two separate variables:
- Number of hours estimated to complete the job – assuming it to be x
- The payment per hour of job – assuming it to be y
Now, as per the given information, Don got paid $336 for his estimated time and payment rate. Hence, we can write,
- xy = 336……………… ①
As he took 4 hours more than the original estimated time, he got paid $2 less in every hour. Hence, we can write,
- (x + 4) (y – 2) = 336 ……………….②
Simplifying, we get xy – 2x + 4y – 8 = 336
Replacing the value of xy from equation 1, we get 336 – 2x + 4y – 8 = 336
Or, -2x + 4y = 8
Or, 4y – 2x = 8
Or, 2y – x = 4
Many students get stuck at this point. As they have already replaced the value of xy from the first equation, they feel that they have only one equation with two unknown variables – hence, the question cannot be solved.
If observed closely, one can still solve the equation by replacing the value of either x or y from the 1st
equation into this derived equation to get the answer.
From equation 1 we can write:
- x = (336/y)
replacing the value of x in the derived equation, we get:
- 2y – (336/y) = 4
Or, 2y² – 336 = 4y
Or, 2y² – 4y – 336 = 0
Or, y² – 2y – 168 = 0
Or, y² – 14y + 12y – 168 = 0
Or, (y – 14) (y + 12) = 0
As y cannot be negative, y = 14
- Replacing the value of y in the equation x = (336/y), we get x = 24
Now, this whole calculation may take longer time than expected and there exist high chances of making errors in different steps involved in the calculation.
Important Observations
- Primarily this question does not need the usage of two variable. The question asks for the estimated time required for the job and only this can be assumed as the variable for the solving purpose.
- While solving the values for x and y, the value of y should not be solved. The question asks for x only, therefore, x should be solved on the first attempt.
Correct approach and solution
We can assume the estimated time for Don to complete the job is t hours.
- Therefore, the originally estimated earnings per hour = (336/t)
- As Don took 4 hours extra, his earnings per hour become [336/(t+4)]
We know, the new earnings per hour are $2 less than the originally estimated earnings per hour Hence, we can write:
- [(336/t) – (336/(t+4))] = 2
Simplifying, we get t² + 4t – 672 = 0
- At this point, one can also form an equation and solve that to get the answer. However, if solving becomes difficult, one can also replace the options in place of t in the equation [(336/t) – (336/(t+4))] = 2, to get the answer
The value of t = 24 will satisfy the equation, hence, the answer is 24 hours.
The devil is in the details! Planning out the finer details of your study schedule takes you one step closer to your target GMAT score. Learn the other benefits of a well defined study plan in this article.
Save 60+ hours of GMAT preparation by crafting a well-defined study plan in just 3 steps:
Mistake number 3 – incorrect interpretation of the question statement
Let’s look at an illustrative example to understand this mistake better.
Example 4
A, B, and C, working individually, can complete a job in 10 days, 12 days, and 15 days respectively. All of them started working on the job together. B left after 2 days. C left 2 days before the originally scheduled number of days at which the job was supposed to be completed. In how many days the job completed?
Solution
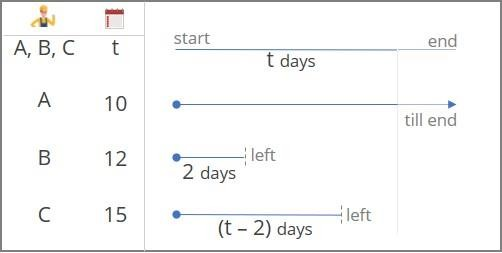
A common approach used by students
In this question, it is given that:
- A, B, and C can complete a certain job in 10, 12, and 15 days respectively while working individually
- All of them started working on the job together
- B left after working for 2 days
- C left 2 days before the originally scheduled work completion time
We need to find out the total number of days at which the work gets completed.
Now, we can assume the total work to be LCM (10, 12, 15) = 60 units
- A can complete 60 units of work in 10 days
- Hence, A can complete 6 units of work in 1 day
- B can complete 60 units of work in 12 days
- Hence, B can complete 5 units of work in 1 day
- C can complete 60 units of work in 15 days
- Hence, C can complete 4 units of work in 1 day
Now, let’s assume the total work gets completed in d days
Hence, we can say
- A works for d days
- B works for 2 days
- C works for (d – 2) days
As we know the work done by them individually in 1 day, we can calculate the total work done by them.
- Work done by A = 6 × d units = 6d units
- Work done by B = 5 × 2 units = 10 units
- Work done by C = 4 × (d – 2) units = 4d – 8 units
Therefore, 6d + 10 + 4d – 8 = 60
- Solving, 10d = 58
- Or, d = 5.8 days
Hence, the total work gets completed in 5.8 days
If you have got 5.8 days as the answer, then you have solved it incorrectly.
The mistake and the correct approach
Here the mistake lies in the wrong interpretation of the question statement.
In the solution, we assumed that the total number of days taken to complete the job is d days. From that, it is inferred that the number of days C worked for is (d – 2) days.
However, in the question, it was mentioned that C left 2 days before the originally scheduled number of days at which the job was supposed to be completed.
- One needs to notice that d days doesn’t indicate the originally scheduled work completion time, rather it indicates the modified work completion time
- The originally scheduled work completion time indicates the time in which the work would have been completed if all A, B, and C worked together till last
Now, the total work done by all 3 of them together in 1 day = (6 + 5 + 4) units = 15 units
Hence, the originally scheduled work completion time = (60/15) days = 4 days
Therefore, C worked for (4 – 2) days = 2 days in total
Hence, we can say
- Work done by A = 6 × d units = 6d units
- Work done by B = 5 × 2 units = 10 units
- Work done by C = 4 × 2 units = 8 units
Therefore, 6d + 10 + 8 = 60 Solving, 6d = 42
Or, d = 7 days
The total work gets completed in 7 days’ time
Takeaways | GMAT Problem Solving | Time and Work
- For any person or machine, efficiency and work rate are always inversely proportional to each other. Hence, less number of resources working in a specific job always take more time compared to more number of resources working on the same job.
- While attempting GMAT problem solving questions on time and work, you need to focus on the exact parameter which the question is asking for. Sometimes assuming more than what is required can complicate the calculation and increase the chance of making an error.
- While making inferences from the question stem, you need to decipher the correct meaning of the given statements and ensure the details are considered while solving – ignoring which may interpret wrongly and get an incorrect answer.
If you are planning to take the GMAT, we can help you with a personalized study plan and give you access to quality online content to prepare. Write to us at acethegmat@e-gmat.com. We are the most reviewed GMAT prep company on gmatclub with more than 2400 reviews and are the only prep company that has delivered more than 700+ scores than any other GMAT club partner. Why don’t you take a free trial and judge for yourself?
Practice questions on Time and Work
Here is a list of questions specifically designed to help you apply the learnings on GMAT problem solving questions on Time and Work












