Want to test your grasp over GMAT Number Properties? Try this 650 level question!
Question
If p is a positive integer such that the greatest common divisor of p and 10 is 2, what is the value of p?
- 150 multiplied by p is the square of an integer
- p/3 is a prime number
Answer Choices:
- Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- EACH statement ALONE is sufficient.
- Statements (1) and (2) TOGETHER are NOT sufficient.
Correct Answer: B
Solution
Did you get this question right? Good Job! You did better than most GMAT aspirants! And, if you didn’t, then read on to figure where you went wrong.
You should solve any Data Sufficiency question using the 5- Step Process we delineate below. That ways, you’ll never make any of the common mistakes that students commit while solving DS questions.
Steps 1 and 2: Understand the question and draw inferences
The question statement tells us the following pieces of information:
- p is a positive integer
- The greatest common divisor of p and 10 is 2
So, this means that:
p is a positive integer such that:
- 2 is a factor of p => p is even
- 5 is NOT a factor of p
Step 3: Analyse Statement 1 independently
Statement 1 tells us that:
150 multiplied by p is the square of an integer
In order to process this information, we should first determine the prime factors of 150.
How do we do that? By drawing a prime factorization tree.
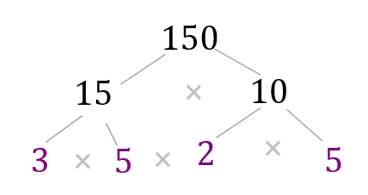
150 = 2 X 3 X 52
We are given that 150p is the square of an integer.
This means that all the prime factors of 150p have even powers.
Of course, this means that p = 2 X 3 = 6
This value of p also satisfies our two tests for p:
- p is even
- p is not divisible by 5
So, Yipee! We found that Statement 1 is sufficient to give us a unique value of p.
Don’t be so excited, dear friend!
If this is how you analysed Statement 1, you fell into the trap that many GMAT aspirants have fallen in before you- making an unfounded assumption about an unknown.
Your calculation of p = 6 would indeed have been correct, had you been told that p is the smallest integer which when multiplied by 150 gives a perfect square
But you have not been told this.
So, p could have many other values for which 150p can be a perfect square.
Some examples are:
23 X 33
23 X 33 X 72
p cannot have values like:
2 X 3 X 52
or
23 X 33 X 52
because in Steps 1 and 2, we have determined that p is not divisible by 5.
So, we can say that, any value of p in which 2 and 3 have an odd power and all other prime factors (none of which is 5) have an even power, will satisfy Statement 1.
Thus, Statement 1 is not sufficient to arrive at a unique value of p.
Step 4: Analyse Statement 2 independently
Statement 2 tells us that:
p/3 is a prime number
=> p = 3 * (a prime number)
From Steps 1 and 2,
We know that p is even.
Thus, the unknown prime number can only be 2.
So, p = 2 X 3 = 6
Thus, Statement 2 alone is sufficient to arrive at a unique value of p.
Step 5: Analyse both statements together (if required)
We do this step only in cases where neither Step 3 nor Step 4 have given us a unique solution. In this question, we arrived at a unique solution in Step 4. So, we do not need to do Step 5.
Answer
Thus, we see that the correct answer choice for this question is B – Statement 2 alone is sufficient but Statement 1 alone is not sufficient.
Key Takeaways
Many questions on GMAT are deceptively easy. They are designed to make you fall right into the trap the question maker set for you! So, beware of making unfounded assumptions about the unknown. Stick only to the information given to you.
Why limit your learning to only this one takeaway? A whole session of exciting GMAT 700+ level questions, deadly traps and “Aha!” takeaways awaits you this Saturday.
- Register for eGMAT’s Free Session on Number Properties here
For those who have already registered, try out the free Number properties concept in our free trial.














