The word Algebra was derived from the Arabic word “al-jabr” meaning “reunion of broken parts”. In algebra, arithmetic computations are carried out with letters standing for numbers. Many students find algebra difficult and through this article, we aim to demystify GMAT Algebra and how you can solve GMAT Algebra questions with ease.

Simple Algebraic expression
The basics of algebra start with understanding simple algebraic expressions. In this section, we will learn more about the different terms & the terminologies used in algebraic expressions.
Algebraic expression:
An algebraic expression is made up of:
- Constants, such as 2, 3, 4, 5, etc,
- Variables, such as (a, b, c, d, …, x, y, x) and,
- Algebraic operations, such as addition, subtraction, multiplication, etc.
Simple examples of algebraic expression are: 2x + 3, 3y + 2, x² + 3 etc.
Terminologies used in an algebraic expression
An algebraic expression includes:
1. Terms
For example: In the expression 9x + 4y + 2
- 9x, 4y, and 2 are three terms.
2. Variable
x and y are variables in the equation 9x + 4y + 2 as their value is not defined.
3. Constant
2 is a constant term in the equation 9x + 4y + 2 as it has one unique and defined value.
4. Coefficient of a variable
The constant attached to the variable is known as the coefficient of the variable.
- In the expression 9x + 4y + 2,
- Coefficient of x = 9
- Coefficient of y = 4
5. Degree
In algebra, the highest power of the variable is known as the degree of the expression.
For example:
| Expression | Degree |
| x² + 2 | 2 (Power of x) |
| x + y³ + 2 | 3 (Power of y) |
| 3x + 4y | 1 (Power of x or y) |
Note:
- If the degree of an algebraic expression is 1 then it is called linear expression.
- If the degree of an algebraic expression is 2 then it is called quadratic expression.
Algebraic Equation
When an expression is equal to a constant/ another expression then an equation is obtained.
For example: 5x and 3x + 4 are two different expressions.
- While 5x = 3x + 4 is one equation.
- Similarly, 4y + 5 = 2 is also an equation.
The solution of an equation
The solution of an equation is the value of the variable for which expression on the left-hand side is equal to the expression on the right-hand side.
For example:
- For y = −3/4 , 4y + 5 is equal to 2
- How we arrived at y = −3/4 will be discussed later in this article.
Linear Equations

Algebraic equations of degree one are called linear equations.
For example: 3x + 9 = 0, a + 2b + 3c = 0 etc.
A linear equation can be either in one variable or more than one variable.
- 3x + 9 = 0 is a linear equation in one variable.
- And, a + 2b + 3c = 0 is a linear equation in three variables.
The most common linear equation involves either one variable or two variables.
Let us learn how to solve both types of linear equations.
Linear equation in one variable
The standard form of linear equation in one variable is ax + b = 0 where a ≠ 0.
- And, it is very easy to find the solution to this type of linear equations.
Solving a Linear equation in one variable
To solve a linear equation of one variable:
- We can move the constant terms to one side and variable terms to another side of the equality sign.
- For example: 2x + 3 = 2 can also be written as:
- 2x = 2 − 3 by moving 3 to the other side of the equality sign.
- Hence, 2x = −2
- x = −1
That is how we can easily solve the linear equations in one variable.
Linear equation in two variables
The standard form of linear equation in two variables is: ax + by + c = 0 where a, b ≠ 0.
For example:
- x + 2y = 3 Or 3x + 4y = 6 etc.
- Both the equation involves two variables: x and y.
Note:
To solve linear equation in two variables, we need two distinct equations to find the value of both the variables.
Let us understand how we can solve these types of equations.
Solving a Linear equation in two variables
Linear equation in two variables can be solved by two methods:
- Substitution Method
- Elimination method
Substitution Method
As the name suggests, in this method:
- We find the value of one of the variables in terms of another variable from one of the equations.
- Then, we substitute the value of that variable in another equation and get an equation in one variable only.
- From this equation, we can find the value of one variable.
- Now, substitute this value in any of the equations to get the value of another variable.
For example:
We have two equations: x + 3y = 4 and x + y = 2.
- We will find the value of either x in terms of y or y in terms of x from one equation.
- We will use x + y = 2 to get x = 2 − y
- Let us now substitute this value of x in another equation i.e. x + 3y = 4
- (2 − y) + 3y = 4
- 2 + 2y = 4
- y = 1
- Substituting y = 1 in x + y = 2, we get x = 1.
That is how we use the substitution method.
Elimination Method
In this method, we first eliminate one of the variables by using algebraic manipulation such as addition, subtraction, multiplication, etc to get the equation in one variable form.
- And, once we have the value of one variable, we can easily find the value of another variable.
Let us take the example of
- x + 3y = 4 ——— Equation 1
- and x + y = 2 ——– Equation 2
and solve it by the elimination method.
We can eliminate either x or y.
By eliminating y
- As the coefficient of y is 3 in equation 1 and 1 in equation 2, we can multiply equation 2 by 3 so that the coefficient of y becomes equal in both equations.
- Multiplying equation 2 by 3, we get:
- 3x + 3y = 6 ——– Equation 3
- On subtracting equation 1 from equation 2, we get
- (3x + 3y) − (x + 3y) = 6 – 4
- 2x = 2 or x = 1
- Substituting x = 1 in x + y = 2, we get y = 1.
- Multiplying equation 2 by 3, we get:
By eliminating x
- As the coefficient of x is 1 in both the equations, it can be eliminated by subtracting both the equations.
- After completing the process, we will get x = 1 and y = 1.
That is how we use the substitution method.
So, we have learnt how to solve linear equations in one variable and two variables.
Let us now understand another type of algebraic equation i.e. Quadratic Equation.
Quadratic Equations
Algebraic equations of degree two are quadratic equations.
For example: x² + 9 = 0, y² + 3y + 2 = 0 etc.
The standard form of a quadratic equation is: ax² + bx + c = 0 where a ≠ 0.
For example:
1. For x² + 3x + 5 = 0,
a) a = 1, b = 3 and c = 5.
2. For y² + 9y + 8 = 1
a) a = 1, b = 9 and c = 7.
b) c is not 8 as y² + 9y + 8 = 1 is not in the standard form of ax² + bx +c = 0.
(i) The standard form is y² + 9y + 7 = 0 (RHS must be 0)
Root of a quadratic equation
Roots of a quadratic equation are nothing but the solutions of the quadratic equation.
- So, the value of a variable that satisfies a quadratic equation is a root of the quadratic equation.
A quadratic equation can have a maximum of two real roots.
- It can have 0 or 1 or 2 roots.
We can find the roots of a quadratic equation by two methods:
- Factor Method
- Quadratic Formula
Factor method
To factor a quadratic equation, ax² + bx + c = 0:
Step 1)- We need to take two numbers such that their sum/difference is b and product is ac.
- For example: For x² + 4x + 3 two such numbers are 3 and 1 as 3 + 1 = 4 and 3 × 1 = 3.
Step 2)- Write the middle term as the sum or difference of the two numbers.
- We can write 4x as 3x + x.
- x² + 4x + 3 = x² + 3x + x + 3
Step 3)- Factor the first two terms and last two terms.
- First two terms are: x² + 3x. This is factored as x (x + 3)
- Last two terms are: x + 3. This is factored as 1 (x +3)
- Hence, x² + 3x + x + 3 = x (x + 3) + 1 (x +3)
Step 4)- Now both the terms should have a common factor. Take that common factor out.
- (x+3) is common in x (x + 3) and 1 (x + 3)
- Hence, x (x + 3) + 1 (x + 3) = (x + 3) (x + 1)
So, this complete process is the factor method.
Hence, the quadratic equation becomes (x + 3) (x + 1) = 0
Now, the product of (x + 3) and (x + 1) = 0 can be 0 only in two cases:
Case-1) When x + 1 is 0
- x = −1
Case-2) When x + 3 is 0
- x = −3.
Hence, −1 and −3 are the roots of x² + 4x +3.
Note:
Both the terms cannot be 0 because x + 3 is definitely greater than x + 1.
This is the complete process of factoring method.
- This method may seem a bit lengthy but the step that takes time is step 1 and once it is done remaining steps are a cakewalk.
Quadratic formula
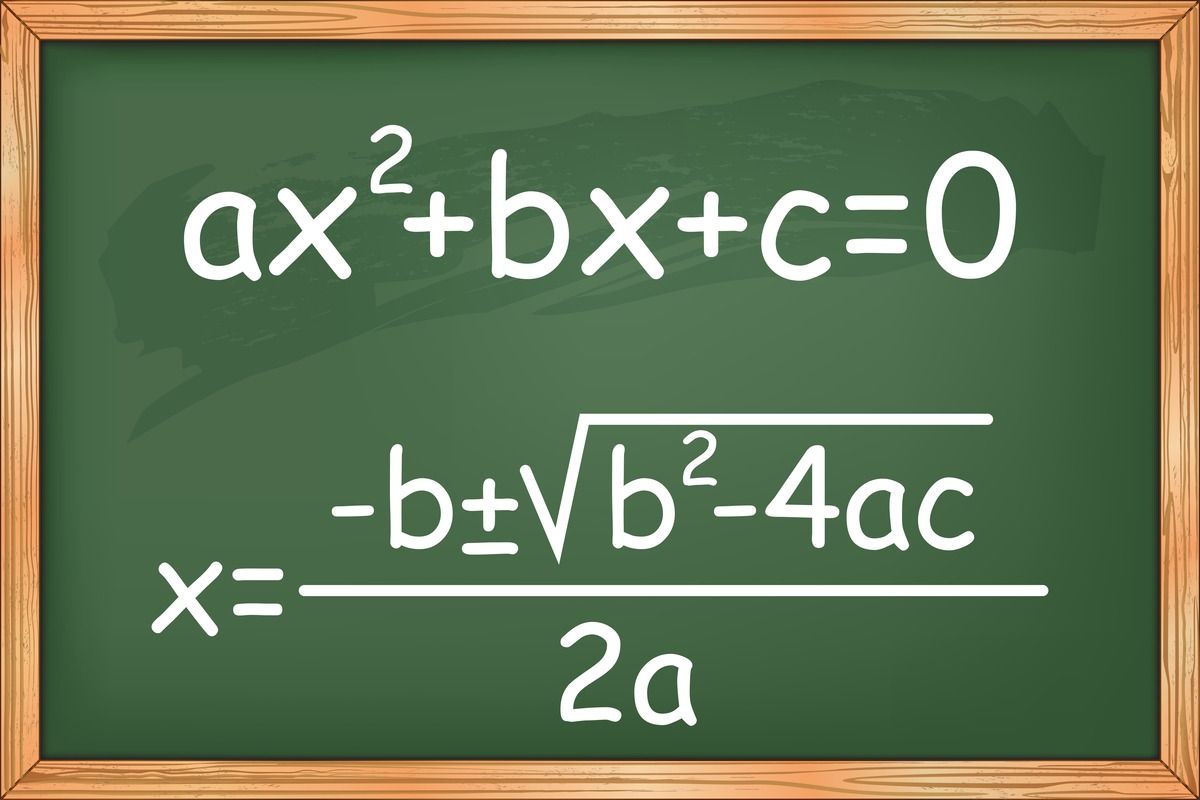
The root of any quadratic equation can be easily obtained by applying the formula:
- x= −b ± √ (b² − 4ac) / 2a, where −b + √ (b² − 4ac) / 2a is one root and −b − √ (b² − 4ac) / 2a is another root.
For example: Let us try finding the roots of the equation x² + 4x +3 by using the quadratic formula.
- In x² + 4x + 3, a = 1, b = 4, and c = 3
- So, roots = −4 ± √ (4² − 4 × 1 × 3) / 2 × 1
- x = (−4 ± 2) / 2 = −2 ± 1
- Hence, −1 and −3 are two roots of the equation.
If you like this article, do check out our other articles on GMAT Quant Topics:
GMAT Algebra Practice Questions

GMAT Algebra Question 1
Which of the following is one of the roots of an equation 3x² + x − 4?
- −4
- −3
- −1
- +1
- +4
Solution
Step 1: Given
- We are given a quadratic equation 3x² + x − 4.
Step 2: To find
- One of the roots of the equation among the given roots.
Step 3: Approach and Working out
3x² + x − 4 = 3x² + 4x − 3x − 4
- x (3x + 4) − 1 (3x + 4)
- (3x + 4 ) (x − 1)
- Hence, x = 1, −4/3.
Thus, the correct answer is option D.
GMAT Algebra Question 2
What is the value of x + y that satisfies the equation 3x + 5y = 16 and x + 2y = 6 ?
- 2
- 3
- 4
- 5
- 6
Solution
Step 1: Given
We are given two linear equations:
- 3x + 5y = 16
- x + 2y = 6
Step 2: To find
- Sum of x and y that satisfies 3x + 5y = 16 and x + 2y = 6.
Step 3: Approach and Working out
3x + 5y = 16 ————–Equation 1
x + 2y = 6—————– Equation 2
By substitution method:
From equation 2, x = 6 − 2y
On substituting x = 6 − 2y in equation 1, we get: 3 (6 − 2y) + 5y = 16
- 18 − 6y + 5y = 16
- 18 − y = 16
- y = 2
Substituting y = 2 in equation 2, we get: x + 4 = 6
- x = 2
Elimination Method:
On multiplying equation 2 by 3, we get: 3x + 6y = 18 —————– Equation 3
Subtracting equation 1 from equation 3, we get: y = 2
Substituting y = 2 in equation 2, we get: x + 4 = 6
- x = 2
Hence, x + y = 4
Thus, the correct answer is option C.
If you are planning to take the GMAT, we can help you with a personalized study plan and give you access to quality online content to prepare. Please write to us at acethegmat@e-gmat.com. We are the most reviewed GMAT prep company on GMAT club with more than 2200 reviews and are the only prep company that has delivered more than 700+ scores than any other GMAT club partner. Why don’t you take a free trial and judge for yourself?















