OG 2020: Question No. 332
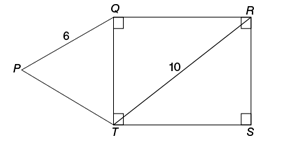
In the figure above, what is the area of region PQRST?
- PQ = RS
- PT = QT
| Source | OG 2020 |
| Type | Data Sufficiency |
| Topic | Geometry |
| Sub-Topic | Quadrilateral/Triangle |
| Difficulty | Medium – Hard. |
Solution
Steps 1 & 2: Understand Question and Draw Inferences
In this question, we are given
- A diagram, consisting of ΔPQT and quadrilateral QRST.
- PQ = 6
- RT = 10
- Also, each angle in the quadrilateral QRST is 90°.
- Hence, QRST is a rectangle.
We need to determine
- The area of the region PQRST.
To determine the area, we need to know the individual area of ΔPQT and quadrilateral QRST.
With this understanding, let us now analyse the individual statements.
Step 3: Analyse Statement 1
As per the information given in statement 1, PQ = RS.
Therefore, PQ = RS = 6.
Now, ΔRST is a right-angled triangle, where RS = 6 and RT = 10
- Therefore, TS = √(102 – 62) = 8
- So, the area of the rectangle QRST = 6 * 8 = 48
- However, we have no information about the side PT of the triangle.
- Thus, we cannot determine the area of ΔPQT
Hence, statement 1 is not sufficient to answer the question.
Step 4: Analyse Statement 2
As per the information given in statement 2, PT = QT.
- However, we do not know the exact value of PT or QT.
Hence, statement 2 is not sufficient to answer the question.
Step 5: Combine Both Statements Together (If Needed)
Combining all the information present in both statements, we get
- Area of rectangle QRST = 48
- PQ = QT (= RS) = PT = 6
- Therefore, ΔPQT is an equilateral triangle with side length 6.
- Hence, area of ΔPQT = (√3/4) * 62
As we can determine the area of both the triangles and quadrilaterals, we can determine the area of the given region.
Hence, the correct answer is option C.
If you are planning to take the GMAT, we can help you with a personalized study plan and give you access to quality online content to prepare. Write to us at acethegmat@e-gmat.com. We are the most reviewed GMAT prep company on gmatclub with more than 2400 reviews and are the only prep company that has delivered more than 700+ scores than any other GMAT club partner. Why don’t you take a free trial and judge for yourself?










