Introduction
Can x⁴ + x² + 1 ever be < 0? Think fast, quant-conqueror!
Got the answer?
If yes, let’s see how this simple question that helps you understand the given expression can help you solve a tricky Quant-based question. If no, don’t worry. As you read further, you will see how you can get to this answer, once you try your hand at the DS question given:
Question
What is the value of x?
Can x⁴ + x² + 1 ever be < 0? Think fast, quant-conqueror!
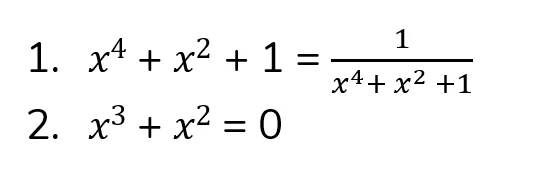
A. (1) ALONE is sufficient, but (2) alone is not sufficient.
B. (2) ALONE is sufficient, but (1) alone is not sufficient.
C. TOGETHER are sufficient, but NEITHER ALONE is sufficient.
D. EACH ALONE is sufficient.
E. NEITHER ALONE NOR TOGETHER is the statements sufficient.
Solution
Statement 1
Statement 1 seems difficult to simplify.
However, if you check the LHS, you have:
- x4 which will be ≥ 0 for any value of x
- x2 which will be ≥ 0 for any value of x
o So, when you add two non-negative entities to 1, the sum will be ≥ 1.

Now, if LHS = RHS, it can only be so if LHS = RHS = 1 (Inference 3)
I guess you know what the next step will be now? Yes, to find the value of x for which LHS = RHS = 1.
Just by looking at it, you know that it is possible only for x = 0.
Thus, statement 1 is sufficient to find the value of x.
Statement 2
You can now solve statement 2:
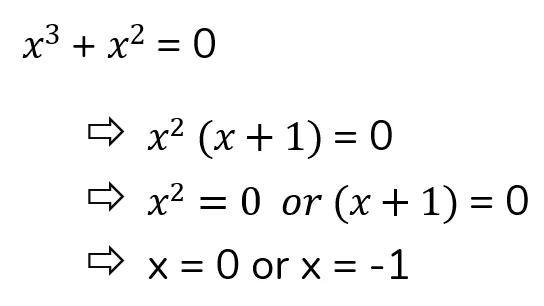
So, as per statement 2, two values are possible for x. Hence, statement 2 is not sufficient.
Hence, the correct answer is A – (1) ALONE is sufficient, but (2) alone is not sufficient.
Conclusion
The example we just solved illustrates a fundamental principle of GMAT Quant: when faced with complex expressions, your first instinct shouldn’t be to dive into algebraic manipulation. Instead, step back and analyze what the expression tells you about possible values and relationships- draw inferences. Remember, in quant problems, looking for these fundamental mathematical properties can save you valuable time and lead you to the correct answer more quickly. Practice identifying these patterns to enhance your problem-solving skills and boost your performance in quantitative sections.
Practice Question
Try this tricky question out:
What is the value of integer x?
1. x5 + x3 + x > 0
2. x2 + 1 = 37
A. (1) ALONE is sufficient, but (2) alone is not sufficient.
B. (2) ALONE is sufficient, but (1) alone is not sufficient.
C. TOGETHER are sufficient, but NEITHER ALONE is sufficient.
D. EACH ALONE is sufficient.
E. NEITHER ALONE NOR TOGETHER is the statements sufficient.
Please present your analysis for this question.














