A 3 min read

“I knew how to solve it, but I messed up the counting!”

This is the most common regret we hear from GMAT test-takers about probability questions. Not concepts, not formulas – just simple counting. Even 700+ scorers admit to double-counting cases or missing possibilities entirely. But what if counting cases could be as simple as filling boxes in a grid? What if you could solve any GMAT probability question with zero chance of missing or double-counting cases?

Let’s Master This Method Step by Step

Warm-up Question

If x is chosen from {1,2} and y is chosen from {3,4}, how many different pairs (x,y) will give an even product?

Take a moment to solve this before reading further. Got your answer? Let’s solve it using a method that will forever change how you tackle such questions.

1. The Matrix Method Solution

1. 1. First, create a simple matrix:
   • Put x values (1,2) as column headers
   • Put y values (3,4) as row headers

1. 2. Fill in the matrix:
   • Multiply each x with each y
   • Mark ‘E’ where you get even products

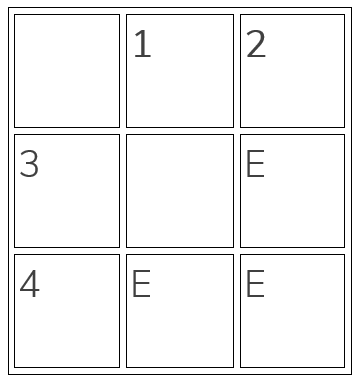
1. 3. Count the results:
   • Count all E’s: we have 3 cases
   • These represent the pairs (1,4), (2,3), and (2,4)

Here is the process summary:

Official GMAT Example

Let’s try our hand at this Medium Level question.

If x is to be chosen at random from the set {1, 2, 3, 4} and y is to be chosen at random from the set {5, 6, 7}, what is the probability that xy will be even?

1. 1/6
2. 1/3
3. 1/2
4. 2/3
5. 5/6

Step-by-Step Solution

1. Create the matrix:

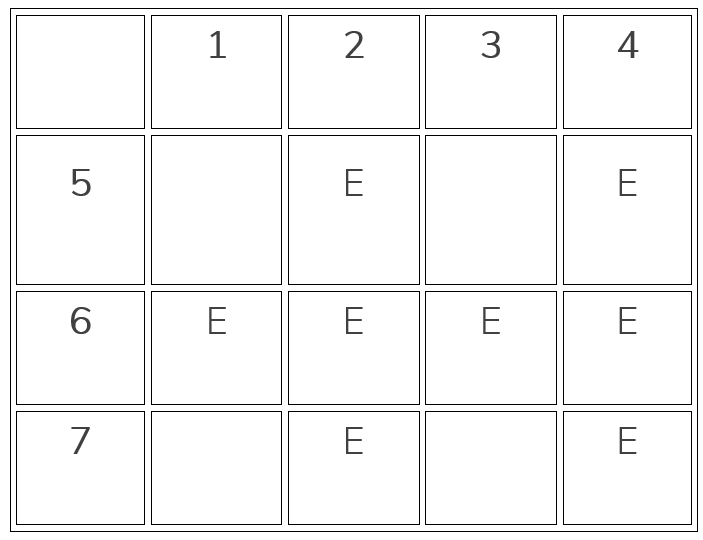
2. Count favorable outcomes:

–> Count E’s: 8 cases where the product is even

3. Calculate total outcomes:

–> Total pairs possible = 4 × 3 = 12

4. Calculate probability:

–> Probability = 8/12 = 2/3

–> Answer: D

Common Trap Alert!

Many students select Choice E, i.e., 5/6 because they count

• both (2,6) and (6,2) as possible outcomes
• both (4,6) and (6,4) as possible outcomes.

Remember: x can only be chosen from the first set and y from the second set. The matrix automatically prevents this mistake!

2. Alternate Approach: The Listing Method

Many students prefer listing out cases systematically. While this method can work, it requires extra care to avoid missing cases. Here’s how to do it carefully:

Step-by-Step Solution

1. Fix x = 1, list all products:
   • 1 × 5 = 5 (odd)
   • 1 × 6 = 6 (even) ✓
   • 1 × 7 = 7 (odd) Cases so far: 1
2. Fix x = 2, list all products:
   • 2 × 5 = 10 (even) ✓
   • 2 × 6 = 12 (even) ✓
   • 2 × 7 = 14 (even) ✓ Cases so far: 4
3. Fix x = 3, list all products:
   • 3 × 5 = 15 (odd)
   • 3 × 6 = 18 (even) ✓
   • 3 × 7 = 21 (odd) Cases so far: 5
4. Fix x = 4, list all products:
   • 4 × 5 = 20 (even) ✓
   • 4 × 6 = 24 (even) ✓
   • 4 × 7 = 28 (even) ✓ Total even cases: 8
5. Calculate probability:
   • Total possible outcomes = 4 × 3 = 12
   • Probability = 8/12 = 2/3
   • Answer: D

Why Students Often Get This Wrong

1. Random listing instead of fixing one variable
2. Missing cases like 4 × 7 = 28 (it’s less obvious that it’s even)
3. Forgetting to count the total possible outcomes
4. Double-counting some cases, such as (6,2) because of random listing.

While this method works, it’s more prone to errors than the matrix method. Use it only if you’re very comfortable with systematic listing.

Remember: In the GMAT, it’s not just about getting the right answer—it’s about getting it right consistently under time pressure. Choose your method wisely!

Key Takeaways for the Matrix Method

• Draw a matrix whenever you need to count pairs
• Each box = exactly one possible outcome
• Can’t miss cases – every possibility has its own box
• Can’t count twice – each box is counted exactly once
• Remember: x and y are from specific sets – don’t swap positions

---

Pro Tips

• Accuracy Boost: In our experience, this method has reduced counting errors by nearly 100%.
• Quick Check: After marking E’s, quickly scan each row. Any pattern you notice can help verify your counting.

Want to master this method? Head to the comments section below for a hard practice question that will help cement your learning.