OG 2020: Question No. 322
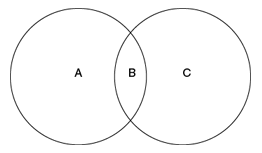
In the figure above, if A, B, and C are the areas, respectively, of the three nonoverlapping regions formed by the intersection of two circles of equal area, what is the value of B + C?
- A + 2B + C = 24
- A + C = 18 and B = 3
| Source | OG 2020 |
| Type | Data Sufficiency |
| Topic | Geometry |
| Sub-Topic | Circle |
| Difficulty | Medium |
Solution
Steps 1 & 2: Understand Question and Draw Inferences
In this question, we are given
- A diagram of two circles, intersecting at two distinct points.
- The areas of the three nonoverlapping regions are denoted as A, B, and C.
- The individual areas of the two circles are equal.
We need to determine
- The value of B + C.
As the individual areas of both circles are equal, we can say
- A + B = B + C
Or, A = C
As we cannot infer any further information from the question stem, let us now analyse the individual statements.
Step 3: Analyse Statement 1
As per the information given in statement 1, A + 2B + C = 24
We also know that A = C.
- Hence, we can write C + 2B + C = 24
Or, 2B + 2C = 24
Or, B + C = 12
As we can determine the value of B + C, statement 1 is sufficient to answer the question.
Step 4: Analyse Statement 2
As per the information given in statement 2, A + C = 18, and B = 3.
We also know that A = C.
- Hence, we can write C + C = 18
Or, C = 9
From this statement, we know the value of B and can determine the value of C.
- Therefore, we can determine the value of B + C.
Hence, statement 2 is sufficient to answer the question.
Step 5: Combine Both Statements Together (If Needed)
Since we could determine the answer from either of the statements individually, this step is not required.
Hence, the correct answer is option D.
If you are planning to take the GMAT, we can help you with a personalized study plan and give you access to quality online content to prepare. Write to us at acethegmat@e-gmat.com. We are the most reviewed GMAT prep company on gmatclub with more than 2400 reviews and are the only prep company that has delivered more than 700+ scores than any other GMAT club partner. Why don’t you take a free trial and judge for yourself?










