OGQR 2020: Question No. 88
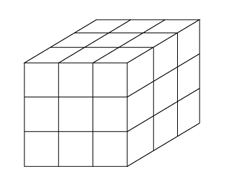
Each of 27 white 1-centimeter cubes will have exactly one face painted red. If these 27 cubes are joined together to form one large cube, as shown above, what is the greatest possible fraction of the surface area that could be red?
| Source | OGQR 2020 |
| Type | Problem Solving |
| Topic | Geometry |
| Sub-Topic | Cube |
| Difficulty | Hard |
Solution
Given
In this question, we are given
- Each of 27 white 1-centimeter cubes will have exactly one face painted red.
- These 27 cubes are joined together to form one large cube, as shown in the given diagram.
To Find
We need to determine
- The greatest possible fraction of the surface area that could be red.
Approach & Working
To maximize the surface area, count as red, except the cube which is at the centre, all the other cubes must have their red surface area exposed.
- Number of cubes with red surface area exposed = 27 – 1 = 26
However, in each surface of the bigger cube, there will be 9 smaller cube surfaces, and there will be total 6 surfaces for the bigger cube.
- Hence, total number of cube surfaces exposed = 9 * 6 = 54
- Therefore, the greatest fraction = 26/54 = 13/27
Hence, the correct answer is option B.
If you are planning to take the GMAT, we can help you with a personalized study plan and give you access to quality online content to prepare. Write to us at acethegmat@e-gmat.com. We are the most reviewed GMAT prep company on gmatclub with more than 2400 reviews and are the only prep company that has delivered more than 700+ scores than any other GMAT club partner. Why don’t you take a free trial and judge for yourself?










