A 2 min read

OG 2020: Question No. 329

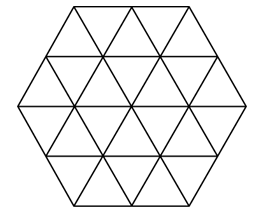
A six-sided mosaic contains 24 triangular pieces of tile of the same size and shape, as shown in the figure above. If the sections of tile fit together perfectly, how many square centimetres of tile are in the mosaic?

1. Each side of each triangular piece of tile is 9 centimetres long.
2. The mosaic can be put inside a rectangular frame that is 40 centimetres wide.

Source	OG 2020
Type	Data Sufficiency
Topic	Geometry
Sub-Topic	Triangle
Difficulty	Medium – Hard

Solution

Steps 1 & 2: Understand Question and Draw Inferences

In this question, we are given

• A diagram showing a six-sided mosaic, contains 24 triangular pieces of tile of the same size and shape.
• The sections of tile fit together perfectly.

We need to determine

• The number of square centimetres of tile, which are in the mosaic.
  • Therefore, we need to know the area of the mosaic.

Since we are not given any other relevant information in the question stem, let us analyse the question statements.

Step 3: Analyse Statement 1

“Each side of each triangular piece of tile is 9 centimetres long.”

We are given that each side of each triangle is 9 cm.

• Hence, each triangle is an equilateral triangle.
  • Thus, we can find the area of each of the 24-equilateral triangle or the mosaic.

Thus, statement 1 is sufficient to answer the question.

Step 4: Analyse Statement 2

“The mosaic can be put inside a rectangular frame that is 40 centimetres wide.”

• For the mosaic to fit, its largest length i.e. AE must fit in the rectangle.
  • Hence, the width of rectangle must be greater than or equal to AE.
    • Therefore, AE ≥ 40
  • However, we do not know the exact value of AE.

Thus, statement 2 is not sufficient to answer the question.

Step 5: Combine Both Statements Together (If Needed)

Since we can determine the answer from statement 1 individually, this step is not required.

Hence, the correct answer choice is option A.

If you are planning to take the GMAT, we can help you with a personalized study plan and give you access to quality online content to prepare. Write to us at acethegmat@e-gmat.com. We are the most reviewed GMAT prep company on gmatclub with more than 2400 reviews and are the only prep company that has delivered more than 700+ scores than any other GMAT club partner. Why don’t you take a free trial and judge for yourself?