OGQR 2020: Question No. 94
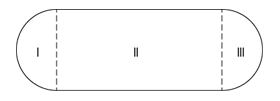
In the racetrack shown above, regions I and III are semi-circular with radius r. If region II is rectangular and its length is twice its width, what is the perimeter of the track in terms of r?
| Source | OGQR 2020 |
| Type | Problem Solving |
| Topic | Geometry |
| Sub-Topic | Circle / Rectangle |
| Difficulty | Medium |
Solution
Given
In this question, we are given
- The diagram of a racetrack consists of two semi-circular regions, with radius r, and one rectangular region.
- The length of the rectangular region is twice its width.
To Find
We need to determine
- The perimeter of the track, expressed in terms of r.
Approach & Working
The perimeter of each semi-circular region = πr
- Therefore, the perimeter of both semi-circular regions together = 2πr
The rectangular region has length twice its width.
- Width of the rectangular region = diameter of the semi-circular region = 2r
- Hence, length of the rectangular region = 2 * 2r = 4r
Therefore, the perimeter of the whole region = 2πr + 4r + 4r = 2πr + 8r = 2r (π + 4)
Hence, the correct answer is option B.
Did you know a 700+ GMAT Score can increase your chances to get into your dream business school? We can help you achieve that. Why don’t you try out our FREE Trial? We are the most reviewed online GMAT Preparation company in GMATClub with more than 1970 reviews as of December 2020.