OGQR 2020: Question No. 85

In the figure above, the area of the parallelogram is
| Source | OGQR 2020 |
| Type | Problem Solving |
| Topic | Geometry |
| Sub-Topic | Quadrilateral |
| Difficulty | Medium |
Solution
Given
In this question, we are given
- The diagram of a parallelogram, where the adjacent sides are of length 8 and 12
- One angle between the sides is 60°
To Find
We need to determine
- The area of the parallelogram
Approach & Working
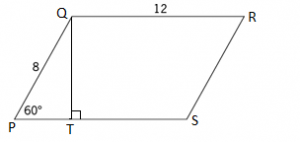
Let us assume the parallelogram is PQRS, and QT is the perpendicular dropped from point Q to the side PS.
- Hence, we can say that PQT is a 30°-60°-90° triangle, and the side ratio is 1: √3: 2.
- QT: PQ = √3: 2
Or, QT = √3/ 2 * PQ = √3/ 2 * 8 = 4√3
- Therefore, the area of the quadrilateral = PS * QT = 12 * 4√3 = 48√3 (PS = QR)
Hence, the correct answer is option D.
Did you know a 700+ GMAT Score can increase your chances to get into your dream business school? We can help you achieve that. Why don’t you try out our FREE Trial? We are the most reviewed online GMAT Preparation company in GMATClub with more than 1950 reviews as of October 2020.














