OG 2020: Question No. 335
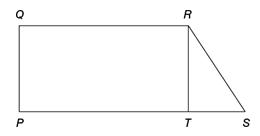
In the figure above, PQRT is a rectangle. What is the length of segment PQ?
- The area of region PQRS is 39 and TS = 6.
- The area of region PQRT is 30 and QR = 10.
| Source | OG 2020 |
| Type | Data Sufficiency |
| Topic | Geometry |
| Sub-Topic | Quadrilateral |
| Difficulty | Medium |
Solution
Steps 1 & 2: Understand Question and Draw Inferences
In this question, we are given
- A diagram of a quadrilateral PQRS, of which PQRT is a rectangle
We need to determine
- The length of segment PQ
Since PQRT is a rectangle we can say the side QR and PT are parallel to each other.
- Therefore, we can say that PQRS is a trapezium.
With this understanding, let us know analyse the individual statements.
Step 3: Analyse Statement 1
As per the information given in statement 1, the area of region PQRS is 39 and TS is equal to 6.
- Area of PQRS = (1/2) (QR + PS) (PQ) = 39
Or, (QR + PS) (PQ) = 78
Or, (PT + PT + TS) (PQ) = 78
Or, (2PT + 6) (PQ) = 78
As we don’t know the value of PT, we cannot determine the value of PQ.
Hence, statement 1 is not sufficient to answer the question.
Step 4: Analyse Statement 2
As per the information given in statement 2, the area of region PQRT is 30 and QR is equal to 10.
- PQ * QR = 30
Or, PQ * 10 = 30
Or, PQ = 3
As we can determine the value of PQ, statement 2 is sufficient to answer the question.
Step 5: Combine Both Statements Together (If Needed)
Since we can determine the answer from statement 2 individually, this step is not required.
Hence, the correct answer choice is option B.
Questions on Geometry are very commonly asked on the GMAT. Ace GMAT Quant by signing up for our free trial and get access to 400+ questions. We are the most reviewed online GMAT Prep company with 2400+ reviews on GMATClub.










