Here’s a scenario that happens every test day: A brilliant student encounters a complex optimization question with 5 variables and multiple constraints. They understand the math perfectly. They set up the equations correctly. But then they make a single logical error about what “optimization” actually means—and get the entire question wrong.
This isn’t a knowledge problem. It’s a strategic thinking error that trips up some of the smartest test-takers.
The most dangerous part? These errors feel logical in the moment. Students think they’re making sound analytical decisions, but they’re actually falling into sophisticated reasoning traps that the GMAT deliberately exploits.
Today, I’m going to show you the exact optimization errors that cause smart students to fail complex TPA questions—and give you the systematic frameworks that transform multi-variable chaos into organized victories.
Key Takeaways from This Optimization Guide:
Smart students fall into optimization traps because they apply logical-sounding but incorrect reasoning. You’re likely wondering:
- Why do “bigger is better” assumptions lead to wrong answers?
- How can systematic frameworks eliminate complex algebraic calculations?
- What strategic thinking patterns prevent optimization errors?
This guide reveals the exact error patterns and provides systematic frameworks to master complex optimization scenarios.
The “Bigger Is Better” Disaster: When Logic Betrays You
Let me start with a real example that illustrates the most common optimization trap.
Official Question: A farmer wants to allocate her expenditures to maximize her profits during the coming year. Let C be her spending on cropland, F her spending on fertilizer, L her spending on labor, M her spending on machinery, and S her spending on seed. She has estimated that, if she allocates at least 100 euros to each of these categories, then her profit during the coming year will be (C – 97)(L – 92)(S – 95)(M – 87)(F – 90) euros. She wishes to calculate the benefits of expenditure greater than 100 euros in one of these categories, if she were to spend exactly 100 euros in each of the others.
Select the resource for which each euro of spending beyond 100 euros is predicted to make the GREATEST contribution to profits, and the resource for which each euro is predicted to make the LEAST contribution.
Here’s where smart students make their fatal error.
The Logical-Sounding Mistake
Students look at the baseline calculation when everything is at €100:
- C – 97 = 3
- L – 92 = 8
- S – 95 = 5
- M – 87 = 13
- F – 90 = 10
Then they think: “If I increase machinery from €100 to €101, M goes from 13 to 14. That’s the biggest number, so it should have the biggest impact on the product.”
This reasoning sounds completely logical. It’s also completely wrong.
The Product Maximization Reality
Here’s what actually happens when you increase each variable by €1:
Increase Cropland (C) to €101:
- Original: 3 × 8 × 5 × 13 × 10 = 15,600
- New: 4 × 8 × 5 × 13 × 10 = 20,800
- Impact: +5,200
Increase Machinery (M) to €101:
- Original: 3 × 8 × 5 × 13 × 10 = 15,600
- New: 3 × 8 × 5 × 14 × 10 = 16,800
- Impact: +1,200
⭐ Key Insight: The counterintuitive truth: Increasing the SMALLEST factor (cropland) has the GREATEST impact on profit. Increasing the LARGEST factor (machinery) has the LEAST impact.
Why this happens: In product maximization, the impact of changing one factor depends on the SIZE of all the other factors combined. When you change the smallest number, you’re multiplying that change by all the larger numbers. When you change the largest number, you’re multiplying by all the smaller numbers.
The Optimization Framework: Systematic Multi-Variable Analysis
The farmer question reveals a critical principle that applies to all complex optimization scenarios:
The Factor Impact Analysis Method
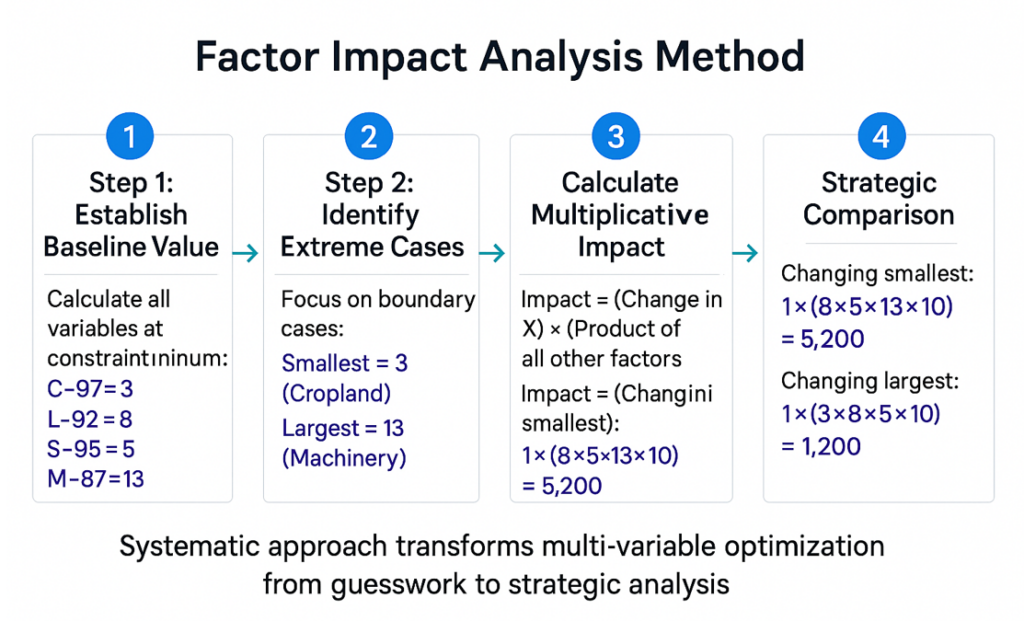
Step 1: Establish Baseline Values
Calculate all variables at their constraint minimums:
- C – 97 = 3
- L – 92 = 8
- S – 95 = 5
- M – 87 = 13
- F – 90 = 10
Step 2: Identify Extreme Cases
Instead of testing all variables, focus on the boundary cases:
- Smallest baseline factor: 3 (Cropland)
- Largest baseline factor: 13 (Machinery)
Step 3: Calculate Multiplicative Impact
For product optimization, the impact of changing factor X is:
Impact = (Change in X) × (Product of all other factors)
Step 4: Strategic Comparison
- Changing smallest factor: 1 × (8 × 5 × 13 × 10) = 5,200
- Changing largest factor: 1 × (3 × 8 × 5 × 10) = 1,200
Answer: Greatest returns = Cropland, Least returns = Machinery
⭐MASTER TPA OPTIMIZATION
Access our Free GMAT Prep Resources including comprehensive TPA strategy lessons, 400+ practice questions, and systematic frameworks for complex optimization scenarios.
The Sequential Budget Trap: Multi-Year Complexity
Now let’s tackle an even more sophisticated optimization challenge—one that combines sequential constraints with dynamic budgeting.
Official Question: A manufacturing company plans to begin automating production by installing industrial robots at the start of each year over five years. Each robot will result in annual labor-cost savings of €150,000 beginning with the year of its installation and will have an upfront cost of €400,000. For robot installation in Year 1, the company will budget €600,000, plus the total amount of labor costs that will be saved by robotic production in that year. The robot-installation budget for each subsequent year will consist of the total amount of labor costs that will be saved by robotic production in that year plus any money left over from the previous year’s robot-installation budget.
Most students try to solve this with pure algebra. Big mistake.
The Algebraic Quicksand Problem
When students approach this algebraically, they get trapped in a web of interdependent equations:
- Year 1 budget depends on Year 1 installations
- Year 2 budget depends on Year 1 installations AND Year 1 leftover
- Year 3 budget depends on ALL previous installations AND previous leftover
The algebra becomes unmanageable, and students waste 4+ minutes without reaching a solution.
⭐ Strategic insight: This isn’t primarily an algebra problem—it’s a segmentation and modeling problem.
The Segmentation Strategy
Key Insight #1: Robot Cost Segmentation
In the year of installation:
- Installation cost: €400,000
- Same-year savings: €150,000
- Net cost to company: €250,000
In subsequent years:
- Installation cost: €0
- Annual savings: €150,000
- Net benefit to company: €150,000
Key Insight #2: Budget Structure Segmentation
- Year 1 budget: €600,000 + savings (but savings already accounted for in net cost)
- Subsequent years: Previous year savings + previous year leftover
The Year-by-Year Model
Year 1 Analysis:
- Available budget: €600,000 (cash infusion)
- Net cost per robot: €250,000
- Robots installable: €600,000 ÷ €250,000 = 2.4 → 2 robots
- Leftover: €600,000 – (2 × €250,000) = €100,000
Year 2 Analysis:
- Savings from existing robots: 2 × €150,000 = €300,000
- Leftover from Year 1: €100,000
- Total budget: €400,000
- Robots installable: €400,000 ÷ €250,000 = 1.6 → 1 robot
- Leftover: €400,000 – €250,000 = €150,000
Year 3 Analysis:
- Savings from existing robots: 3 × €150,000 = €450,000
- Leftover from Year 2: €150,000
- Total budget: €600,000
- Robots installable: €600,000 ÷ €250,000 = 2.4 → 2 robots
Answer:
- Year 1 installations: 2 robots
- Year 3 total robots in service: 2 + 1 + 2 = 5 robots
The Strategic Framework for Complex Optimization
Based on these examples, here’s your systematic approach to any complex optimization scenario:

Phase 1: Problem Type Recognition (20 seconds)
- Product optimization: Look for multiplicative relationships
- Sequential optimization: Look for time-dependent constraints
- Constraint optimization: Look for boundary conditions and trade-offs
Phase 2: Segmentation Strategy (40 seconds)
- For product problems: Identify factors and their relative magnitudes
- For sequential problems: Break into time periods with distinct characteristics
- For constraint problems: Separate fixed costs from variable impacts
Phase 3: Strategic Modeling (60 seconds)
Create frameworks that eliminate algebraic complexity:
- Net impact calculations (benefits minus costs)
- Extreme case analysis (boundary conditions)
- Sequential tracking (year-by-year or step-by-step)
Phase 4: Systematic Verification (15 seconds)
Check your logic against the problem constraints:
- Do your numbers satisfy all given conditions?
- Does your optimization direction make intuitive sense?
- Have you answered what was actually asked?
Common Optimization Error Patterns (And How to Eliminate Them)

Error Pattern #1: The Linear Thinking Trap
- What it looks like: Assuming that bigger individual numbers always create bigger overall impacts
- Root cause: Confusing additive optimization with multiplicative optimization
- How to fix it: Always calculate the actual impact, never assume based on magnitude alone
Error Pattern #2: The Algebraic Obsession
- What it looks like: Trying to solve complex sequential problems with pure equation systems
- Root cause: Treating dynamic scenarios as static mathematical problems
- How to fix it: Use segmentation and modeling frameworks before resorting to algebra
Error Pattern #3: The Single-Variable Focus
- What it looks like: Optimizing one variable without considering interactions with others
- Root cause: Missing the systemic nature of multi-variable optimization
- How to fix it: Always consider how changes in one variable affect the entire system
Advanced Optimization Confidence Building
Here’s how to develop unshakeable confidence with complex optimization scenarios:
Week 1: Product vs. Sum Discrimination
- Practice 10 questions that mix additive and multiplicative optimization
- For each question, identify whether you’re maximizing sums or products
- Notice how the strategy changes completely based on the mathematical structure
Week 2: Segmentation Skill Development
- Work through sequential constraint problems using segmentation first, algebra second
- Time how much faster segmentation approaches are compared to pure algebraic methods
- Build your framework library for different constraint types
Week 3: Extreme Case Mastery
- For each optimization problem, identify the boundary cases that reveal the pattern
- Practice extracting insights from extreme scenarios rather than testing all possibilities
- Develop intuition for when extreme case analysis provides the fastest path to solutions
⚡Ready to Master TPA Optimization?
Get access to our comprehensive TPA preparation resources including strategic frameworks, 400+ practice questions, and systematic approaches to complex optimization problems.
The Meta-Skill: Strategic Problem Recognition
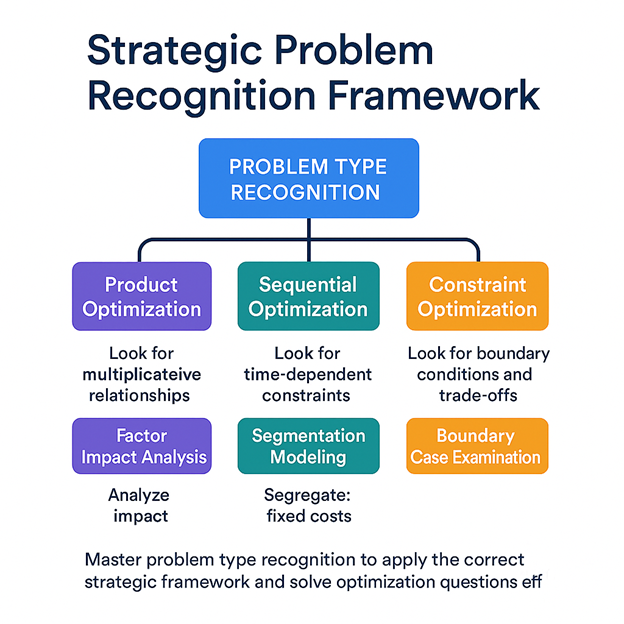
The highest-level skill in optimization isn’t mathematical—it’s recognizing WHICH type of optimization challenge you’re facing and applying the appropriate strategic framework.
| Problem Type | Strategic Approach |
| Product optimization | Factor impact analysis |
| Sequential optimization | Segmentation modeling |
| Constraint optimization | Boundary case examination |
Students who master this meta-skill don’t just solve optimization problems faster—they approach them with confidence because they know exactly which strategic toolkit to apply.
Your Final Challenge
You’ve now learned to avoid the reading disasters that trip up most students, eliminate the inference failures that waste precious time, and navigate the optimization traps that challenge even strong mathematical thinkers.
But there’s one final error pattern that can undo all your technical mastery: the execution errors that occur under time pressure and test day stress.
In our final article, we’ll tackle the time management and execution strategies that ensure your newfound skills translate into actual score improvements when it matters most.
⭐ Practice Assignment: Find 3 complex TPA questions with multiple variables or sequential constraints. Before solving, spend 60 seconds identifying the optimization type and appropriate strategic framework. Notice how this upfront investment makes the actual solving process faster and more accurate.
The students who achieve optimization mastery don’t just calculate better—they think systematically about which calculation approach will be most efficient. Starting now, you do too.
⭐ Transform Your TPA Performance
Ready to eliminate optimization errors and master complex TPA scenarios? Get access to:
- ✅ Comprehensive TPA strategy frameworks
- ✅ 400+ practice questions with detailed explanations
- ✅ Systematic optimization methodologies
- ✅ Free adaptive mock test
- ✅ Expert video lessons on advanced TPA concepts














