Quick Wins: The 90-Second Solutions for GMAT Quants That Save Minutes

A 6 min read

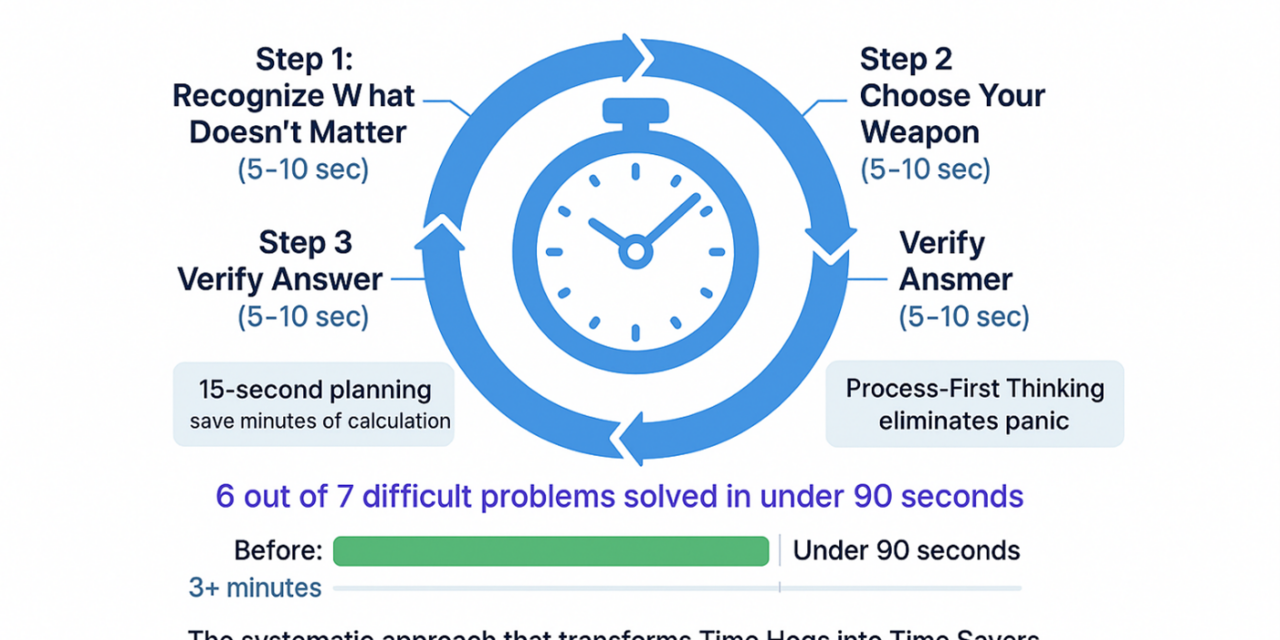
Here’s a startling fact: 6 out of 7 difficult GMAT arithmetic questions are actually Time Savers in disguise. You read that correctly. Those intimidating problems that seem to demand 3+ minutes of calculation? Most can be solved in under 90 seconds once you know the right approach.

Today, I’m going to transform how you see “difficult” GMAT arithmetic. By the end of this article, you’ll possess three powerful techniques that turn complex-looking problems into quick victories. More importantly, you’ll understand why spending 15 seconds planning your approach saves you minutes of unnecessary calculation.

The Power of Simplification—When Less is Exponentially More

Let me show you a problem that stumps most test-takers:

Your first instinct might be to start calculating each expression. Stop. That’s exactly what transforms this Time Saver into a Time Hog.

The 90-Second Solution Path

Step 1: Recognize What Doesn’t Matter (5 seconds)

All expressions have negative signs outside. Since we’re finding the median—the middle value when ordered—these negative signs don’t affect the ordering. Remove them mentally.

Step 2: Apply the Reciprocal Rule (10 seconds)

Negative exponents mean reciprocals. Let me demonstrate with a simpler example: 2^(-2) becomes 1/4. Similarly, (1/2)^(-6/4) becomes 2^(6/4) or 2^(3/2).

Step 3: Convert Everything (20 seconds)

• (1/2)^(-6/4) → 2^(3/2)
• (1/4)^(-2/3) → 4^(2/3) = 2^(4/3)
• (3/6)^(-1/2) → (1/2)^(-1/2) = 2^(1/2)
• (1/3)^(-3/2) → 3^(3/2)
• (1/2)^(-4/2) → 2^2

Step 4: Order and Identify (15 seconds)

With everything in comparable form:

2^(1/2) < 2^(4/3) < 2^(3/2) < 2^2 < 3^(3/2) 

The median is 2^(3/2), which corresponds to the original -(1/2)^(-6/4).

⭐ Answer: A
Total time: Less than 60 seconds.

What transformed this from a calculation nightmare into a quick win? You recognized that complexity was superficial. The negative signs, the fractional bases, the negative exponents—they all simplify away when you see the underlying structure.

Drawing Inferences Beats Calculation

Here’s another problem that appears calculation-heavy:

Most students start listing all even integers from 50 to 100. That’s 26 numbers to analyze. There’s a faster way.

The Inference Approach

Step 1: Translate the Constraint (10 seconds)

If 3^m is a factor of this product, we need to count all factors of 3 in the even integers from 50 to 100. But wait—even integers that contain factors of 3 must be multiples of 6. That’s our inference.

Step 2: List Only What Matters (15 seconds)

Even multiples of 3 in our range: 54, 60, 66, 72, 78, 84, 90, 96

That’s just 8 numbers instead of 26.

Step 3: Extract Factors Systematically (30 seconds)

Factor out one 3 from each:

• 54 = 3 × 18
• 60 = 3 × 20
• 66 = 3 × 22
• 72 = 3 × 24
• 78 = 3 × 26
• 84 = 3 × 28
• 90 = 3 × 30
• 96 = 3 × 32

That’s 8 factors of 3 immediately.

Step 4: Check for Additional Factors (20 seconds)

From the remaining numbers (18, 20, 22, 24, 26, 28, 30, 32), which contain 3?

• 18 = 2 × 3 × 3 (two additional 3s)
• 24 = 3 × 8 (one more 3)
• 30 = 3 × 10 (one more 3)

Total: 8 + 4 = 12 (8 from the first set + 4 additional from 18, 24, and 30)

⭐ Answer: B
Time invested: 75 seconds.

The key insight? You didn’t calculate the product of 26 numbers. You inferred that only multiples of 6 mattered and systematically extracted factors. Actively drawing inferences eliminated 70% of the work.

Formula Mastery for Instant Solutions

Sometimes, the fastest path is knowing exactly which method to use to solve the question:

Picking the Appropriate Method

Step 1: Understand the Structure (10 seconds)

A cube has 6 faces and 8 vertices. At each vertex, exactly 3 faces meet.

Step 2: Set Up the Calculation (10 seconds)

Total ways to choose 3 faces from 6: C(6,3) = 20

Step 3: Identify Invalid Cases (15 seconds)

Invalid selections are those where all 3 faces meet at the same vertex. Since there are 8 vertices and at each vertex exactly 3 faces meet, there are 8 invalid combinations.

Step 4: Calculate (5 seconds)

Valid selections = 20 – 8 = 12

⭐ Answer: C
Total time: 40 seconds.

Notice what we didn’t do? We didn’t try to visualize every possible combination. We didn’t draw elaborate diagrams. We applied a counting principle: Total – Invalid = Valid.

The 15-Second Planning Investment

Here’s what separates those who consistently solve problems in 90 seconds from those who struggle for 3+ minutes: the planning pause.

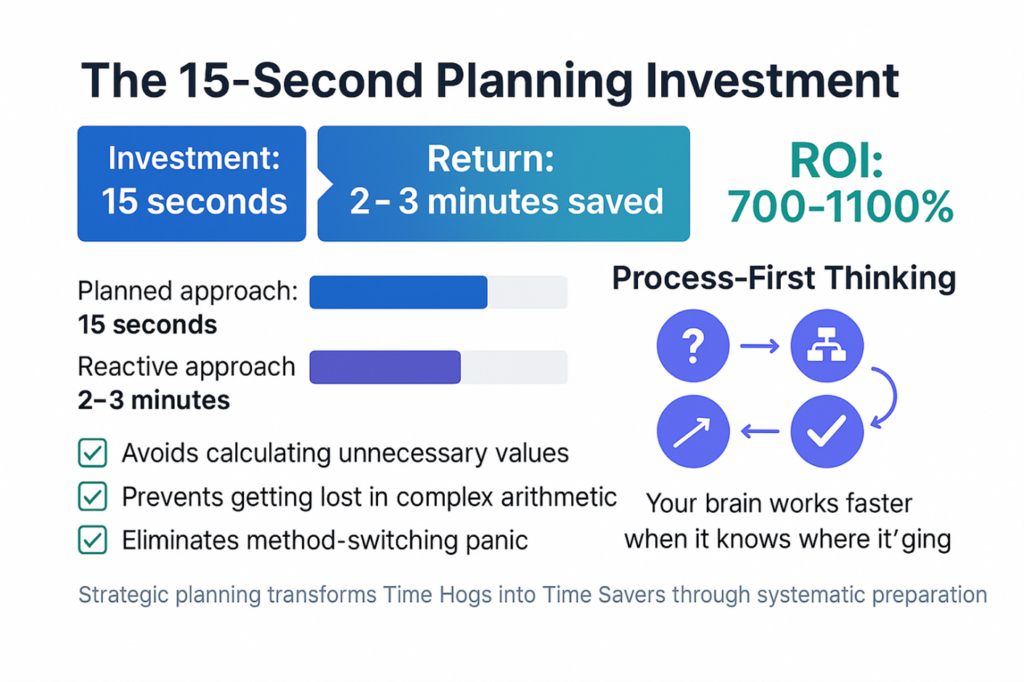
Before you write anything, before you calculate anything, take 10-15 seconds to:

• Identify the Core Challenge: What makes this problem appear difficult?
• Choose Your Weapon: Simplification? Drawing Inferences? Retrieving the applicable concept?
• Map Your Path: What are your steps going to be?

This isn’t wasted time. When you invest these 15 seconds upfront, you avoid:

• Calculating unnecessary values
• Getting lost in complex arithmetic
• Realizing halfway through that there’s an easier method
• The panic that comes from watching time slip away

⭐ Key Insight: We call this “Process-First Thinking”—a cornerstone of our Own the Dataset methodology. Your brain works faster when it knows where it’s going.

Your 90-Second Transformation Toolkit

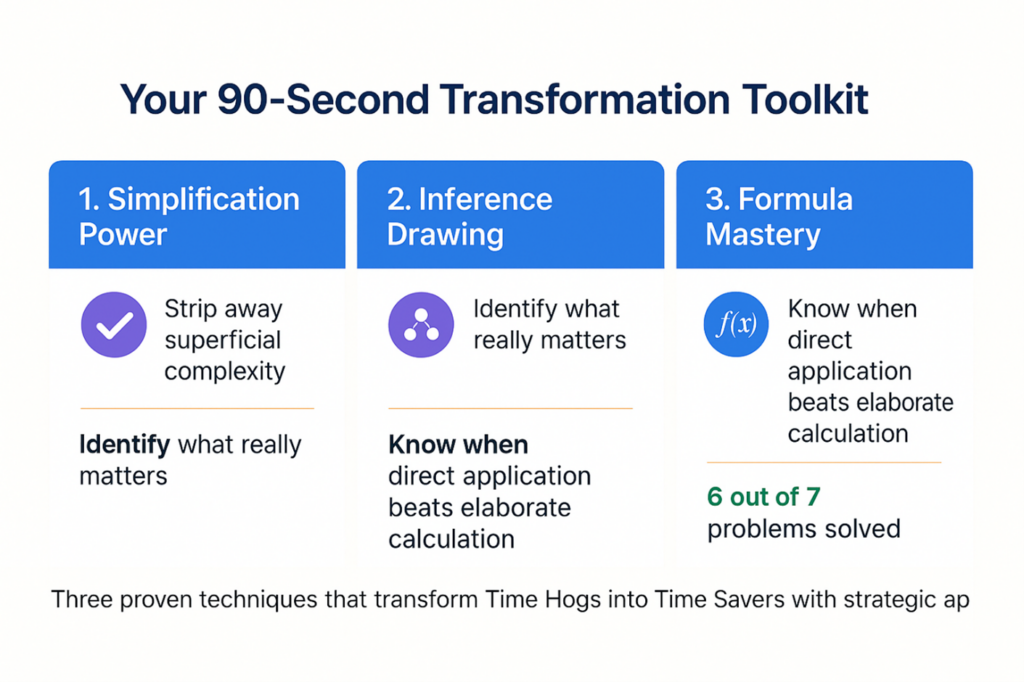
You now possess three powerful techniques for rapid problem-solving:

1. Simplification Power: Strip away superficial complexity to reveal simple structures
2. Inference: Identify what really matters and ignore the rest
3. Formula Mastery: Know when direct application beats elaborate calculation

But more importantly, you understand the meta-skill: that 15-second planning pause that transforms Time Hogs into Time Savers.

⭐ Remember this: In our analysis of difficult GMAT arithmetic questions, only 1 in 7 genuinely requires extended calculation time. The other 6? They’re waiting for you to see through their disguise.

What’s Next?

In our next article, “Strategic Solvers—The 2-3 Minute Champions,” we’ll tackle problems that require slightly more sophisticated approaches—the work rate problems and probability scenarios that benefit from systematic visualization. You’ll learn when to build tables, when to draw grids, and when strategic setup time pays massive dividends.

For now, practice these three techniques. Take that planning pause. Transform those intimidating problems into quick victories.

➡️ Final Thought: Speed on the GMAT isn’t about calculating faster—it’s about recognizing when you don’t need to calculate at all.