OGQR 2020: Question No. 220
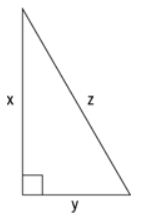
If A is the area of a triangle with sides of lengths x, y, and z as shown above, what is the value of A?
- z = 13
- A = 5y/2
| Source | OGQR 2020 |
| Type | Data Sufficiency |
| Topic | Geometry |
| Sub-Topic | Triangles |
| Difficulty | Medium |
Solution
Steps 1 & 2: Understand Question and Draw Inferences
In this question, we are given:
- A right-angle triangle of area A
- Side lengths of the triangle are: x, y, and z.
We need to find:
- The value of A.
Now, the given triangle is a right-angled triangle.
- Hence, its area A = 1/2 * xy
Therefore, if we know the value of x and y or their product, we can find the value of A.
With this understanding, let us now analyse the individual statements.
Step 3: Analyse Statement 1
“z = 13”
Since we do not get the values of x and y from this statement, statement 1 is not sufficient to answer the question.
Step 4: Analyse Statement 2
“A = 5y/2”
- 1/2 * xy = 5y/2
Or, x = 5
However, we do not know the value of y.
Therefore, statement 2 is not sufficient to answer the question.
Step 5: Combine Both Statements Together (If Needed)
From statement 1: z =13
From statement 2: x = 5
On applying Pythagoras theorem in the given triangle, we get: x2 + y2 = z2
- 52 + y2 = 132
From this equation, we can find y.
- Hence, we can find the value of A.
Since we could find the answer by combining both the statements, option C is the correct answer.














