OGQR 2020: Question No. 219
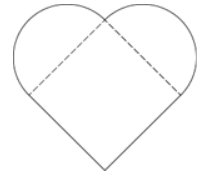
The heart-shaped decoration shown in the figure above consists of a square and two semicircles. What is the radius of each semicircle?
- The diagonal of the square is 10√2 centimetres long.
- The area of the square region minus the sum of the areas of the semi-circular regions is 100 – 25π square centimetres.
| Source | OGQR 2020 |
| Type | Data Sufficiency |
| Topic | Geometry |
| Sub-Topic | Squares/Circles |
| Difficulty | Medium |
Solution
Steps 1 & 2: Understand Question and Draw Inferences
We are given:
- A heart shaped decoration figure.
- It consists: A square and two semicircles.
We need to find:
- The radius of each semicircle.
Let us assume that r is radius of the semicircle.
- Hence, 2r is the side of the square as shown.
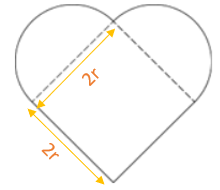
- Therefore, if we know the side of square or any relation by which we can find r, we can find the radius of the semicircle.
With this understanding, let us now analyse the individual statements.
Step 3: Analyse Statement 1
“The diagonal of the square is 10√2 centimetres long.”

- If 2r is the side of the square, then 2r is the length of the diagonal.
- Hence, 2r = 10
- Therefore, we can find the value of r from the above equation.
Hence, statement 1 is sufficient to find the answer.
Step 4: Analyse Statement 2
“The area of the square region minus the sum of the areas of the semi-circular regions is 100 – 25π square centimetres.”
- Area of square – 2 * area of semicircle = (2r)2 – 2 *
- 100 – 25π = 4r2 – πr2 = r2 (4 -π)
- 25(4 – π) = r2 (4 -π)
- r2 = 25
From the above equation, we can find the value of r.
Hence, statement 2 is sufficient to answer the question.
Step 5: Combine Both Statements Together (If Needed)
Since we could determine the answer from either of the statements individually, this step is not required.
Hence, the correct answer is option D.














