A 2 min read

OGQR 2020: Question No. 222

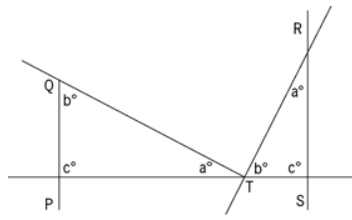
The figure above shows a portion of a road map on which the measures of certain angles are indicated. If all lines shown are straight and intersect as shown, is road PQ parallel to road RS?

Source	OGQR 2020
Type	Data Sufficiency
Topic	Geometry
Sub-Topic	Lines and Angles
Difficulty	Easy – Medium

Solution

Steps 1 & 2: Understand Question and Draw Inferences

In this question, we are given:

• A portion of the roadmap
  • Showing the measures of certain angles.
• All the lines shown in the figure are straight.

We need to find:

• Whether road PQ is parallel to road RS.

Per our conceptual understanding, when two parallel lines are cut by a transversal line then their corresponding angles are equal.

So, If PQ and RS are two parallel lines and line L₁ as shown is the transversal line then the corresponding angles are equal.

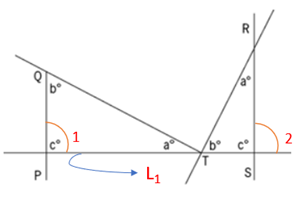
• Hence, ∠1 = ∠2
  • Or, c⁰ = 180⁰ – c⁰
  • 2c = 180
  • c = 90°

Therefore, if we get c = 90° then PQ and RS are parallel else PQ and RS are not parallel,

With this understanding, let us now analyse the individual statements.

Step 3: Analyse Statement 1

“b = 2a”

Per conceptual understanding, the sum of all the angles of a triangle is 180.

• Hence, a + b + c = 180
  • a + 2a + c = 180
  • 3a + c = 180

However, from the above equation, we can get many values of a and c.

Hence, statement 1 is not sufficient to answer the question.

Step 4: Analyse Statement 2

“c = 3a”

• a + b + c = 180
  • a + b + 3a = 180
  • b + 4a = 180

However, from the above equation, we can get many values of a and b.

• Hence, statement 2 is not sufficient to answer the question.

Step 5: Combine Both Statements Together (If Needed)

From statement 1:

• 3a + c = 180

From statement 2:

• c = 3a

Combining both the statements:

• 3a + 3a = 180.

From the above equation, we can find the value of a. Then we can find c.

Since we could find the answer by combining both the statements, option C is the correct answer.

A high GMAT score can set you apart from the competition and help you get an admit at your dream business school. Start your GMAT Preparation with the most reviewed online GMAT prep company. Try out our FREE Trial Today!