OG 2020: Question No. 328
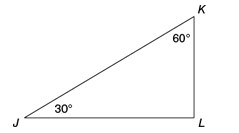
In ΔJKL shown above, what is the length of segment JL?
- JK = 10
- KL = 5
| Source | OG 2020 |
| Type | Data Sufficiency |
| Topic | Geometry |
| Sub-Topic | Triangles |
| Difficulty | Easy – Medium |
Solution
Steps 1 & 2: Understand Question and Draw Inferences
In this question, we are given
- The diagram of a triangle ΔJKL, where angle KJL = 30° and angle JKL = 60°
We need to determine
- The length of the segment JL
As angle KJL = 30° and angle JKL = 60°, we can say angle JLK = 180° – (30° + 60°) = 90°
Hence, ΔJKL is a 30°-60°-90° triangle, and its sides are in the ratio 1: √3: 2.
- Or in other words, KL: JL: JK = 1: √3: 2.
- Therefore, to find the length of any side, we need to know the length of any of the other two sides.
With this understanding, let us now analyse the individual statements.
Step 3: Analyse Statement 1
As per the information given in statement 1, JK = 10.
- Using the side ratio, we can determine the value of JL, with the help of the value of JK.
Hence, statement 1 is sufficient to answer the question.
Step 4: Analyse Statement 2
As per the information given in statement 2, KL = 5.
- Using the side ratio, we can determine the value of JL, with the help of the value of KL.
Hence, statement 2 is sufficient to answer the question.
Step 5: Combine Both Statements Together (If Needed)
Since we could determine the answer from either of the statements individually, this step is not required.
Hence, the correct answer is option D.














