A 2 min read

PQID – DS28502.01 | OG 2020: Question No. 317

If each side of parallelogram P has length 1, what is the area of P?

1. One angle of P measures 45 degrees.
2. The altitude of P is √2/2.

Source	OG 2020
PQID	DS28502.01
Type	Data Sufficiency
Topic	Geometry
Sub-Topic	Quadrilateral
Difficulty	Hard

Solution

Steps 1 & 2: Understand Question and Draw Inferences

In this question, we are given

• Each side of the parallelogram P has length 1.

We need to determine

• The area of the parallelogram P.

To determine the area of the parallelogram, we need to know the base (which is given as 1), and the height of the parallelogram because area of a parallelogram = Base × Height.

• Hence, in this case, we need to know the height of the parallelogram to find its area.

With this understanding, let us now analyze the individual statements.

Step 3: Analyse Statement 1

As per the information given in statement 1, one angle of P measures 45 degrees.

Hence, we can draw the parallelogram as shown:

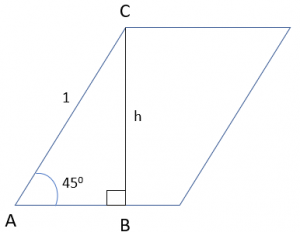
• △ABC is a right-angled triangle as shown.
  • By applying the property that sum of all angles in a triangle is 180⁰, we can say:
    • 90⁰ + 45⁰ + ∠ACB = 180⁰
    • ∠ACB = 45⁰

• Hence, △ABC is a 45 – 45 – 90 triangle.
  • So, AB = BC = h
  • Applying Pythagoras theorem:
    • AC² = AB² + BC²
    • 1 = 2h²
    • So, h = 1/√2

Hence, statement 1 is sufficient to find the answer to the question.

Step 4: Analyse Statement 2

As per the information given in statement 2, the altitude of P is √2/2.

• Hence, h = √2/2 =√2.
• We can find out the area of the triangles.

Hence, statement 2 is sufficient to find the answer to the question.

Step 5: Combine Both Statements Together (If Needed)

Since we can determine the answer from either of the statements individually, this step is not required.

Hence, the correct answer choice is option D.

Takeaways

1. Area of a parallelogram = Base × Height
2. Angle-Sum property of a triangle: Sum of all the angles in a triangle is 180°.

Did you know a 700+ GMAT Score can increase your chances to get into your dream business school? We can help you achieve that. Why don’t you try out our FREE Trial? We are the most-reviewed online GMAT Preparation company in GMATClub with more than 2500 reviews.