Smart vs Hard: “SIMPLIFY” Skills that Transform Impossible into Manageable

A 6 min read

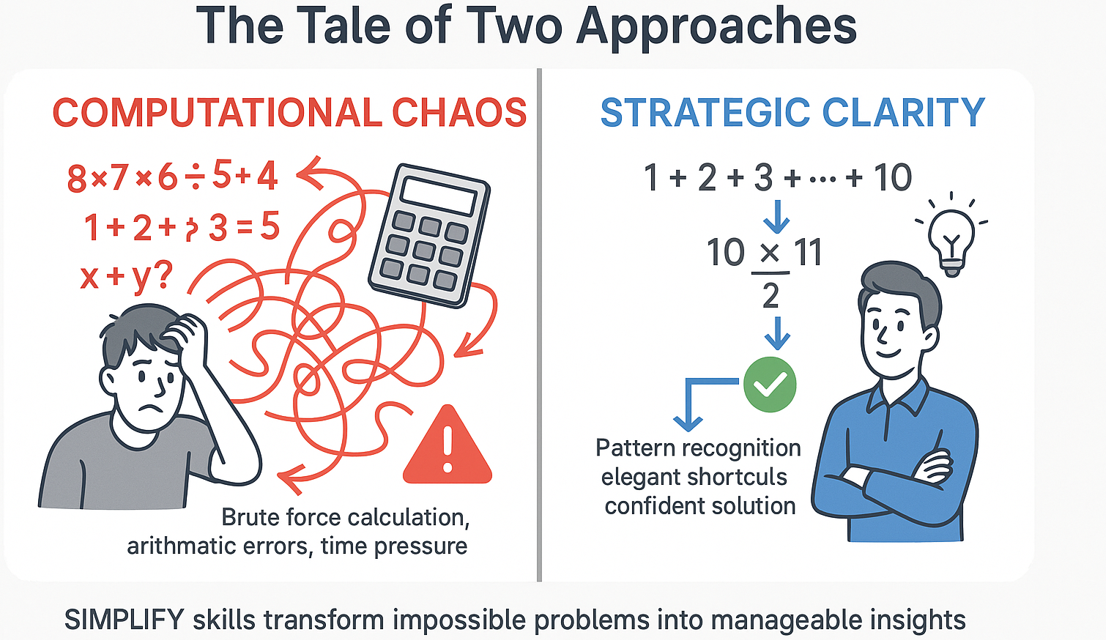
You’re facing a math problem loaded with intimidating numbers, and your mind immediately locks onto one approach: brute-force calculation. Your brain starts mapping out an arithmetic battle plan—multiply these massive numbers, compute exact values, slog through every single step of the computational nightmare ahead.

But as you dive into the calculations, something terrible happens. The numbers get unwieldy. The arithmetic becomes error prone. What started as a clear path forward dissolves into a mess of mistakes, crossed-out work, and growing panic as precious test time slips away.

Here’s what most students don’t realize: that computational complexity isn’t the real challenge—it’s a distraction from the elegant mathematical insight waiting to be discovered.

That’s the power of SIMPLIFY skills – the ability to see past surface complexity and recognize the elegant structure hiding underneath.

When Students Hit the Computational Wall

Let me introduce you to three students who learned this lesson the hard way.

Priya and the Decimal Disaster

The Problem: {0.99999999}{1.0001}- {0.99999991}{1.0003}= ??

(A) 10^(-8) (B) 3×10^(-8) (C) 3×10^(-4) (D) 2×10^(-4) (E) 10^(-4)

Priya took one look at this monster and thought, “Okay, I need to get these fractions to have common denominators, then subtract.” She started calculating:

“Let me see… the common denominator would be 1.0001 × 1.0003… that’s 1.00040003. Then I need to multiply 0.99999999 by 1.0003… that’s…”

Ten minutes later, Priya is drowning in decimals, making arithmetic errors, and getting nowhere.

❌ Where Priya Hit the Wall: She tried to muscle through with pure computation instead of stepping back to see what these numbers actually represent.

Kenji and the Factorial Fiasco

The Problem: If n = 9! – 6^4, which of the following is the greatest integer k such that 3^k is a factor of n?

(A) 1 (B) 3 (C) 4 (D) 6 (E) 8

Kenji’s approach: “First, let me calculate 9! That’s 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 × 9… let me see… 362,880. And 6^4 = 1,296. So n = 362,880 – 1,296 = 361,584. Now I need to divide this by powers of 3 until it doesn’t work…”

Kenji spent 15 minutes on arithmetic, made several calculation errors, and still had no clear path to the answer.

❌ Where Kenji Hit the Wall: He got buried in huge numbers instead of recognizing that this is really a problem about prime factorizations.

Amara and the Prime Product Panic

The Problem: The product of all the prime numbers less than 20 is closest to which of the following powers of 10?

(A) 10⁹ (B) 10⁸ (C) 10⁷ (D) 10⁶ (E) 10⁵

Amara started listing: “2, 3, 5, 7, 11, 13, 17, 19. Now let me multiply: 2 × 3 = 6, then 6 × 5 = 30, then 30 × 7 = 210, then 210 × 11 = 2,310…”

By the time Amara got to multiplying by 17 and 19, she was dealing with numbers like 510,510 × 19, making errors left and right.

❌ Where Amara Hit the Wall: She tried to compute the exact product instead of realizing this is an estimation problem that doesn’t need precise arithmetic.

The SIMPLIFY Rescue: Seeing Structure, Not Just Numbers

Here’s where the magic happens. Instead of fighting the complexity, what if we SIMPLIFY by recognizing the underlying patterns?

Priya’s Rescue: The “Close to 1” Pattern

Let’s help Priya see what she missed. Look at those decimal numbers again:

• 0.99999999 = 1 – 0.00000001 = 1 – 10⁻⁸
• 0.99999991 = 1 – 0.00000009 = 1 – 9×10⁻⁸
• 1.0001 = 1 + 0.0001 = 1 + 10⁻⁴
• 1.0003 = 1 + 0.0003 = 1 + 3×10⁻⁴

⭐ The Key Insight: Both fractions have the form “something very close to 1” divided by “something slightly bigger than 1.”

When you divide a number slightly less than 1 by a number slightly more than 1, you get approximately: 1 minus the denominator’s extra amount.

So:

• First fraction ≈ 1 – 10⁻⁴
• Second fraction ≈ 1 – 3×10⁻⁴
• Difference = [1 – 10⁻⁴] – [1 – 3×10⁻⁴] = 2×10⁻⁴

⚡ The Magic: Instead of brutal decimal arithmetic, Priya could have solved this in three clean steps by recognizing the structural pattern.

Kenji’s Rescue: The Factoring Strategy

Let’s show Kenji the elegant path. Instead of computing those massive numbers, recognize that both terms share a common structure:

⭐ The Key Insight: Both 9! and 6^4 contain powers of 3. Let’s extract them:

• 9! contains 3, 6(=2×3), and 9(=3×3), giving us 1+1+2 = 4 factors of 3. So 9! = 3⁴ × m
• 6^4 = (2×3)^4 = 2⁴ × 3⁴

Now our subtraction becomes: n = 9! – 6^4 = 3⁴ × m – 3⁴ × 16 = 3⁴(m – 16)

Instead of working with 361,584, Kenji can work with the much simpler difference (m – 16), then check if this difference has additional factors of 3.

⚡ The Magic: By factoring first, Kenji transforms an intimidating arithmetic problem into a manageable factorization analysis.

Amara’s Rescue: The Strategic Grouping Approach

Let’s rescue Amara from her multiplication nightmare. The key is recognizing this as an estimation problem, not an exact calculation problem.

⭐ The Key Insight: Group the primes strategically to create powers of 10:

• 2 × 5 = 10 (perfect!)
• 7 × 11 ≈ 77 ≈ 80 = 8 × 10
• 13 × 17 ≈ 221 ≈ 220 = 22 × 10
• 3 × 19 ≈ 57 ≈ 60 = 6 × 10

Product ≈ 10 × (8×10) × (22×10) × (6×10) = 10 × 8 × 22 × 6 × 10³ = 10,560 × 10³ ≈ 10⁷

⚡ The Magic: Instead of exact multiplication, Amara could estimate the order of magnitude in just a few strategic steps.

The Pattern Recognition Superpower

Notice what all three rescues have in common? They all involve seeing the forest instead of the trees:

• Priya’s problem: Recognize “close to 1” patterns instead of fighting decimals
• Kenji’s problem: Recognize shared prime factors instead of computing huge numbers
• Amara’s problem: Recognize powers of 10 opportunities instead of exact multiplication

This is what SIMPLIFY skills really do – they help you spot the underlying mathematical structure that makes problems manageable.

Your SIMPLIFY Toolkit: Questions to Ask Yourself

When you encounter a computationally intimidating problem, pause and ask:

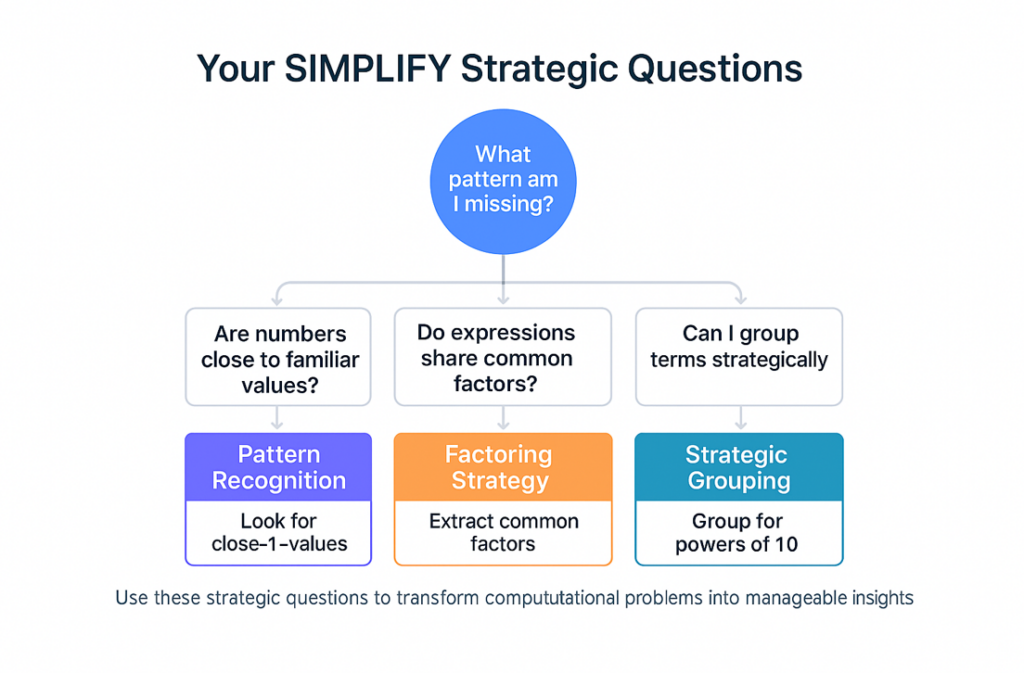
“What pattern am I missing?”

• Are numbers close to familiar values (like 1, 10, 100)?
• Do expressions share common factors I can pull out?
• Can I group terms strategically?

“What is this problem really about?”

• Is this asking for an exact answer or an approximation?
• What mathematical concept is being tested underneath the arithmetic?

“How can I make this smaller?”

• Can I factor out common terms?
• Can I use substitution to work with simpler expressions?
• Can I estimate instead of calculating exactly?

The Transformation: From Computational Victim to Strategic Thinker

Here’s the beautiful truth: The problems that look the most computationally frightening are often the ones with the most elegant shortcuts. The complexity is usually a disguise, not the real challenge.

When you develop strong SIMPLIFY skills, you stop being a victim of arithmetic and become a detective of mathematical structure. You start seeing patterns instead of just numbers. You start recognizing opportunities instead of just obstacles.

The next time a problem tries to bury you in calculations, take a breath and ask: “What would the smart approach look like here?”

⭐ Remember: There’s always a smart approach. Always. And once you find it, you’ll wonder why you ever thought math had to be so hard.