Ever wonder how top scorers breeze through GMAT Quant questions in 2 minutes while you’re stuck for 5+ minutes? The secret lies not in calculating faster, but in calculating smarter. Let’s discover their strategy through a real GMAT question.
The Challenge
Here’s an official GMAT question:
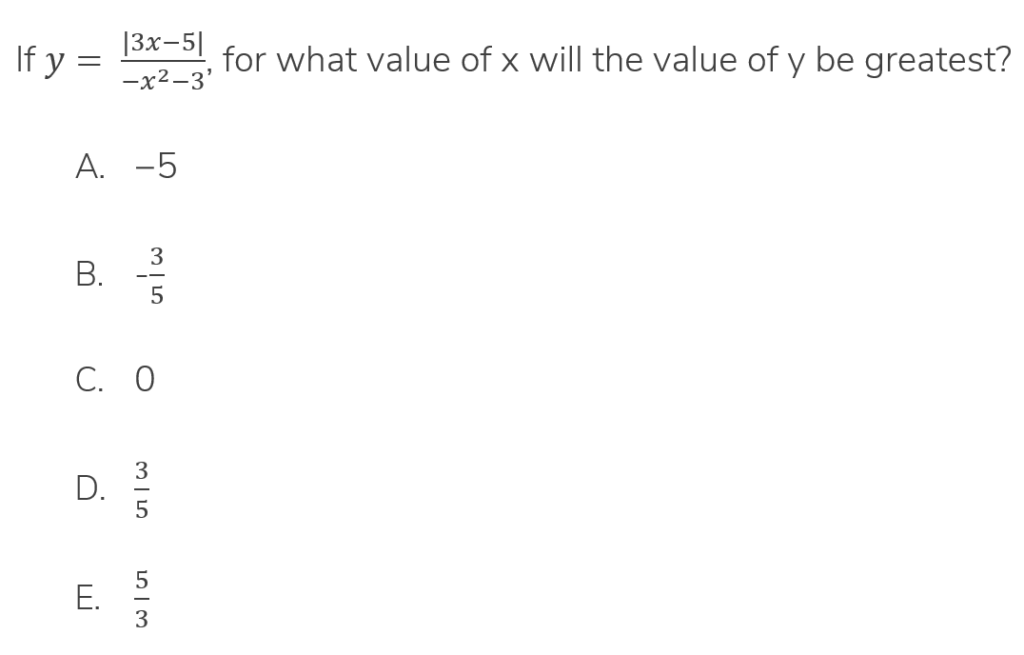
The Tempting (Inefficient) Approach
Your first instinct might be to start plugging in values. Let’s see why that’s a trap:
For x = −5:

Exhausted yet? We haven’t even tested the other four options! Each calculation involves absolute values, negative squares, and complex fractions. There must be a better way…
The Strategic Solution
Instead of diving into calculations, let’s think logically for 30 seconds:
- Analyze the denominator: (−x² − 3)
- −x² ≤ 0 for all real numbers (since squares are non-negative).
- −3 is negative.
- Hence, the denominator is always negative.
- Look at the numerator: |3x − 5|
- |a| ≥ 0 for all real numbers.
- Hence, the numerator is always non-negative.
- Put it together:
–> Therefore, y ≤ 0 for all real x
–> Therefore, max(y) = 0
- Find when y = 0:
- This occurs when numerator = 0
- |3x − 5| = 0
- 3x − 5 = 0
- Therefore, x = 5/3
Looking at our options, there’s 5/3 (E)! ✓
Why This Matters
Compare the two approaches:
Key Strategies for GMAT Success
- Pause Before Computing: Take 30 seconds to analyze the expression before reaching for your pen.
- Draw logical inferences:
- |x| ≥ 0 (absolute values)
- x² ≥ 0 (squares)
- a/b < 0 when a > 0 and b < 0
- Use Logic First: Save substitution as a last resort.
- Be Strategic: If you must substitute:
- Simplify the expressions.
- Choose “easy” numbers first (0, 1, −1).
- Look for numbers that could eliminate multiple options.
The Bottom Line
Remember: GMAT rewards elegant thinking over mechanical calculation. The test makers deliberately design questions where substitution is possible but painfully time-consuming. They’re testing your ability to find smarter solutions.
Key Takeaways
Your time is valuable on the GMAT. Make sure you’re spending it thinking, not just calculating.
Want to cement your understanding with another OG question? Check the comments below. Also, if you want us to help you with a logical solution for any OG question, share the question with us.
Practice Question
A small business has just invested in a new piece of equipment. The business’s accountant estimates that the value of the equipment will decrease over time at a constant rate. Based on this assumption, the accountant properly estimates the value of the equipment 3 years afterward to be $X, 6 years afterward to be $Y, and 8 years afterward to be, for the first time, $0.
Select values for X and for Y that are jointly consistent with the given information. Make only two selections, one in each column.