OGQR 2020: Question No. 217
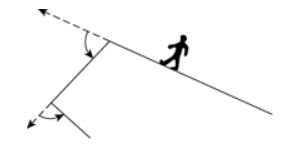
A person walked completely around the edge of a park beginning at the midpoint of one edge and making the minimum number of turns, each with the minimum number of degrees necessary, as shown in the figure above. What is the sum of the degrees of all the turns that the person made?
- One of the turns is 80Ā degrees.
- The number of sides of the park is 4, all of the sides are straight, and each interior angle is less than 180Ā degrees.
| Source | OGQR 2020 |
| Type | Data Sufficiency |
| Topic | Geometry |
| Sub-Topic | Polygons |
| Difficulty | Hard |
Solution
Steps 1 & 2: Understand Question and Draw Inferences
In this question, we are given that:
- A person is walking around the edge of a park.
- He starts walking from the midpoint of one edge of the park.
- The person will make the minimum number of turns with the minimum number of degrees
We need to find:
- The sum of the degrees of the turns made by the person.
To find the sum of degrees made by the person
- We need to find the angles measure on each turn
- And, we need to find how many turn the person takes
- Or, how many sides are there in the park.
With this understanding, let us now analyse the individual statements.
Step 3: Analyse Statement 1
āOne of the turns is 80Ā degrees.ā
From this statement, we cannot know how many sides does the park have neither the angles measure on each turn.
Hence, statement 1 is not sufficient to answer this question.
Step 4: Analyse Statement 2
The number of sides of the park is 4, all of the sides are straight, and each interior angle is less than 180Ā degrees
From this statement, we know that park has 4 sides.
- Hence, it is in the shape of quadrilateral with 4 sides as shown where a, b, c, and d are the internal angles of the quadrilateral.
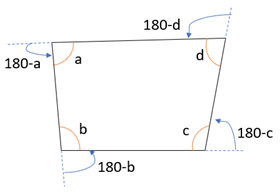
- The curved arrows show the turns taken by the person.
- Hence, the measure of angles in degrees on the turns are 180 ā a, 180 ā b, 180 ā c, and 180 ā d.
- Therefore, the sum of degrees of the turns taken by the person = 180 ā a + 180 ā b + 180 ā c + 180 ā d
- = 4 * 180 ā (a + b + c + d)
- Now, a + b+ c + d = Sum of all the internal angles of the quadrilateral
- Per our conceptual understanding, the sum of the internal angles of a polygon having n sides = (n ā 2) * 180
- Thus, a + b + c + d = (4 ā 2) * 180 = 360
- Therefore, we can find the value of 4 * 180 ā (a + b + c + d).
- = 4 * 180 ā (a + b + c + d)
Hence, statement 2 is sufficient to find the answer.
Step 5: Combine Both Statements Together (If Needed)
Since we could determine the answer from statement 2 individually, this step is not required.
Hence, the correct answer is option B.
