When Math Problems Speak in Code: The TRANSLATE Skill That Cracks Every GMAT Setup Trap

A 6 min read

You know that sinking moment when you finish a math problem, check your calculations twice, and realize with growing dread that your answer isn’t among the choices. Your arithmetic was flawless. Your approach seemed logical. Yet somehow, you’ve arrived at the wrong destination entirely.

If this scenario triggers a familiar knot in your stomach, you’ve experienced the most insidious trap in GMAT math—and it has nothing to do with your calculation abilities.

The Universal Student Nightmare

The brutal truth is that most wrong answers are born in those first crucial seconds when you translate English into mathematical setup. Miss a key phrase, misinterpret a relationship, or set up the wrong equation, and even perfect math becomes a one-way ticket to frustration. But here’s what changes everything: there’s a systematic skill that acts like a universal decoder for problem language, working whether you’re tackling rates, decimals, divisibility, or statistics. Master this TRANSLATE process, and you’ll never again fall victim to those deceptive setup traps that ensnare even strong students.

The Hidden Language Traps (And How They Fool Smart Students)

Let me show you how this works with four problems that look completely different but share the same hidden trap: deceptive problem language that leads to wrong setups.

Problem 1: The Rate Trap

Sarah encounters this problem and thinks she understands it:

Sarah thinks: “Oh, this is asking how much Shannon contributed each minute. So if she listened 10 hours per week, that’s 600 minutes per week. She contributed $35 total, so… wait, is that $35 per week or per year?”

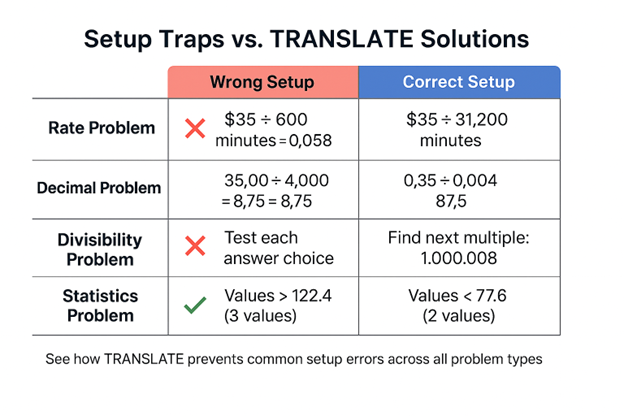
She gets confused about the time periods and ends up calculating $35 ÷ 600 minutes, giving her about $0.058 per minute. She picks answer choice D.

⚠️ Where Sarah Hit the Wall: The phrase “per minute” made her think about a regular payment rate instead of understanding this as asking for a total contribution divided by total listening time. The mixing of “hours per week” with “per minute” in the question scrambled her setup.

Problem 2: The Decimal Place Value Trap

Zara encounters this problem and feels confident:

Zara thinks: “Thirty-five hundredths… that’s 35.00. Four thousandths… that’s 4.000. So I need to calculate 35.00 ÷ 4.000 = 8.75. The tenths digit is 7!”

But wait – Zara just made the classic decimal place value error.

⚠️ Where Zara Hit the Wall: The words “hundredths” and “thousandths” got mixed up with “hundreds” and “thousands” in her mind. Instead of 0.35 ÷ 0.004, she calculated 35.00 ÷ 4.000, leading to a completely wrong setup.

Problem 3: The “Smallest” Confusion Trap

Liam reads this problem and thinks he’s got it:

Liam thinks: “The smallest 7-digit number is 1,000,000. Let me check if that’s divisible by 43…” He calculates 1,000,000 ÷ 43 and gets a remainder. “Hmm, it’s not divisible. Let me try the answer choices…”

He starts testing each answer choice to see which ones are divisible by 43, missing the systematic approach entirely.

⚠️ Where Liam Hit the Wall: He correctly identified what “smallest 7-digit number” means, but didn’t translate “exactly divisible by 43” into the systematic concept of “finding the next multiple of 43 after 1,000,000.”

Problem 4: The Direction Disaster

Emma looks at this statistics problem:

Emma thinks: “More than 1 standard deviation below the mean… so I need to find values that are greater than (mean + 1 standard deviation), right?”

She calculates the mean as 100 seconds, adds 22.4 to get 122.4, and counts how many times are greater than 122.4. She finds three times of 130 seconds and chooses answer C.

⚠️ Where Emma Hit the Wall: The phrase “more than 1 standard deviation below the mean” got scrambled in translation. She interpreted “below” as “above” and set up the inequality in the wrong direction entirely.

Enter the TRANSLATE Skill: Your Universal Decoder Ring

Here’s what all these students were missing: the ability to systematically decode problem language into precise mathematical relationships before jumping into calculations.

Let’s see how TRANSLATE rescues each of these students:

TRANSLATE Rescues Sarah (Rate Problem)

Step 1: Identify key phrases

• “contribution per minute”
• “10 hours per week”
• “last year”

Step 2: Convert to mathematical meaning

• “per minute” = total contribution ÷ total minutes (not a regular payment)
• Need to convert “10 hours per week” to “total minutes for the year”
• “last year” means we need annual totals

Step 3: Check the setup
Setup: $35 ÷ (10 hours/week × 52 weeks/year × 60 minutes/hour) = $35 ÷ 31,200 minutes = $0.00112 ≈ $0.001

✅ Sarah’s reaction: “Oh! I was thinking of ‘per minute’ like a salary rate, but it’s actually asking for the total amount divided by total time. That completely changes the setup!”

TRANSLATE Rescues Zara (Decimal Problem)

Step 1: Identify key phrases

• “thirty-five hundredths”
• “four thousandths”
• “tenths digit”

Step 2: Convert to mathematical meaning

• “hundredths” = second decimal place → 0.35
• “thousandths” = third decimal place → 0.004
• “tenths digit” = first digit after decimal point

Step 3: Check the setup
Setup: 0.35 ÷ 0.004 = 87.5
The tenths digit is 5.

✅ Zara’s reaction: “I was confusing ‘hundredths’ with ‘hundreds’! The word ‘hundredths’ specifically means the 0.01 place, so thirty-five hundredths is 0.35, not 35.00. Completely different problem!”

TRANSLATE Rescues Liam (Divisibility Problem)

Step 1: Identify key phrases

• “smallest 7-digit number”
• “exactly divisible by 43”

Step 2: Convert to mathematical meaning

• “smallest 7-digit number” = 1,000,000 (starting point)
• “exactly divisible by 43” = find next multiple of 43 ≥ 1,000,000

Step 3: Check the setup
Setup: Find remainder when 1,000,000 ÷ 43, then add (43 – remainder)
1,000,000 ÷ 43 = 23,255 remainder 35
Next multiple: 1,000,000 + (43 – 35) = 1,000,008

✅ Liam’s reaction: “I was thinking about this as testing individual numbers, but ‘exactly divisible’ means I need to find the next multiple systematically. Much more efficient!”

TRANSLATE Rescues Emma (Statistics Problem)

Step 1: Identify key phrases

• “more than 1 standard deviation below the mean”
• “below the mean”

Step 2: Convert to mathematical meaning

• “below the mean” = less than the mean (direction)
• “1 standard deviation below” = mean – 1×(standard deviation)
• “more than 1 standard deviation below” = less than (mean – 1×SD)

Step 3: Check the setup

Setup: Find values < (100 – 22.4) = find values < 77.6

Counting: 70 < 77.6 ✓, 75 < 77.6 ✓ → Two values

✅ Emma’s reaction: “I got turned around by ‘below’! When something is ‘below the mean,’ it’s smaller than the mean, so I need the ‘less than’ inequality, not ‘greater than.’ The direction is everything!”

The TRANSLATE Pattern That Works Across All Math

Notice something powerful: The same TRANSLATE process worked across four completely different mathematical contexts – rates, decimals, divisibility, and statistics.

This isn’t a coincidence. Problem language follows patterns, and once you recognize them, you can decode any setup trap:

Your TRANSLATE Action Plan

Before you start calculating on any problem:

1. Circle the tricky descriptive phrases – anything that describes relationships, positions, or comparisons
2. Write out what each phrase means mathematically – don’t just assume you know
3. Set up your mathematical relationship first – before plugging in any numbers
4. Ask yourself: “Does my setup actually answer what they’re asking?”

The beauty of TRANSLATE is that it prevents errors instead of forcing you to find them later. Get the translation right, and your math will lead you to the correct answer. Get it wrong, and even perfect calculations lead to wrong answer choices.

⭐ Key Insight: Math problems aren’t trying to trick you with impossible calculations. They’re testing whether you can decode their language accurately. Master that translation, and setup traps become a thing of the past.

The next time you see problem language that makes you pause and think “wait, what exactly are they asking?” – that’s your cue that TRANSLATE skills are about to save you from a setup trap. Trust the process, decode carefully, and watch your accuracy soar across every type of math problem.